計算理論（その04/X） - 「大人の教養・知識・気付き」を伸ばすブログ

はじめに

Introduction to the Theory of Computation

作者:Sipser, Michael
Course Technology Inc

Amazon

を参照しつつ計算理論を学んでいきます。

前回

power-of-awareness.com

はじめに
前回
1.　正規言語
- 1.2　非決定主義
  - 1.2.1　非決定的有限オートマトンの形式的定義

1.　正規言語

　計算理論はまず「コンピュータとは何か」という問いから始まる。手許にあるノートPCなどのパソコンはコンピュータとしてはあまりに複雑すぎるため、理論的には計算モデル( $computational\ model$ )という理想的なコンピュータを用いる。科学で用いるモデルと同様に計算モデルはある面では正確である一方で、別の面では不正確である。したがって注目したい特徴に応じて異なる複数の計算モデルを扱うことにする。

1.2　非決定主義

　非決定主義は計算理論において大きな衝撃を与えた有用な概念である。以下の議論では差し当たり、計算のすべての段階でそれ以前の段階で一意な方法に従うものとする。コンピュータが所与の状態にあり次の入力文字を読み込んだとき、次の状態が何であるか既知である、すなわち決定付けられている。これを決定的な計算と呼ぶ。非決定的なコンピュータでは、あらゆる点の次の状態にいくつかの選択肢があり得ることになる。
　非決定主義は、決定主義の一般化であり、したがってあらゆる決定主義的な有限オートマトンは自動的に非決定的な有限オートマトンである。非決定的な有限オートマトンは追加的な特徴を持つ。
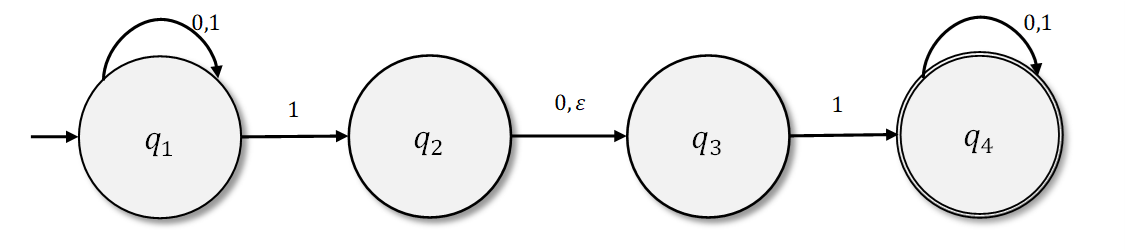
　決定主義的な有限オートマトンとの相違点は、直ちに分かる。まず決定主義的なオートマトン( $\mathrm{DFA}$ )におけるあらゆる状態は、アルファベットにおいて取り得るあらゆるらゆる記号の1つの既存の遷移先を表す。以下で表されるような非決定的有限オートマトンは( $\mathrm{NFA}$ )はその規則を破っている。状態 $q_1$ は $0$ に対して1本の矢印を持つ。しかし $1$ に対しては2つの矢印を持つ。状態 $q_2$ は $0$ に対して1つの矢印を持つが、 $1$ に対しては矢印を持たない。 $\mathrm{NFA}$ では、状態はアルファベット標章に対して $0,1$ 本または多数の矢印を持つことがある。

図表1　非決定的有限オートマトン $N_1$

　2つ目に、 $\mathrm{DFA}$ では遷移矢印のラベルはアルファベットの標章で表される。この $\mathrm{NFA}$ ではラベル $\varepsilon$ に対する矢印を持っている。一般に $\mathrm{NFA}$ はアルファベットに含まれる文字または $\varepsilon$ でラベル付けされた矢印を持つことがある。
　ではどうやって $\mathrm{NFA}$ は計算すればよいのか。ある入力を得た $\mathrm{NFA}$ を動かして進行方向が複数ある状態に至ったと仮定する。たとえば $N_1$ において状態 $q_1$ に至ったとし、次の入力が $1$ だとする。その標章を読み込んだ後、コンピュータはそれ自体複数のコピーに分裂し、遷移し得るすべての先へ同時に進む。コンピュータの各コピーは、進行できるある1つの進行先へ行き、従来通りと同様に更に進んでいく。続けて進める先があるならば、コンピュータはまた分裂する。次の入力がコンピュータのコピーで占められる状態が存在する矢印がどれも現れなかったならば、コンピュータのコピーはそれに紐づく枝と共に消滅する。最後にコンピュータのいずれか1つのコピーが入力の最後に許容状態へ移ったのであれば、 $\mathrm{NFA}$ は入力文字を許容する。
　既存矢印の $\varepsilon$ シンボルを持つ状態に出くわした場合、同様のことが生じる。入力を読み込むことなく、コンピュータは複数のコピーに分裂し、あるものは既存の $\varepsilon$ でラベル付けされた既存の矢印のそれぞれに進み、またあるものは現在の状態に留まる。そのときコンピュータは従来通りに確定的に進んでいく。
　非決定性は、複数の独立した過程やスレッドが同時に進行できる並列計算の一種として見られることがある。 $\mathrm{NFA}$ が複数の選択肢、すなわち分岐点に進むことに対応するがこれらに進むべく分裂したとき、それぞれ分離して進んでいく。
　非決定的計算を考える別の方法には、確率木としてのものである。木の根には計算の開始時点が対応する。あらゆる枝の点は、コンピュータが複数の選択肢を持つような計算におけるある点(状態)を表す。計算枝がに少なくとも1つ許容状態で終わったならば、コンピュータは許容状態に至ったとする。

図表2　出力 $\mathrm{010110}$ における $N_1$ の計算

このように実験し続けることで $N_1$ が部分文字列として $\mathrm{101}$ または $\mathrm{11}$ のいずれかを含む全文字列を許容することが分かる。
　非決定的有限オートマトンはいくつかの面で有用である。あらゆる $\mathrm{NFA}$ はそれと等価な $\mathrm{ＤFA}$ に変換することができ、 $\mathrm{NFA}$ を構築することは時に直接 $\mathrm{DFA}$ を構築するよりも簡単である。 $\mathrm{NFA}$ はそれに対応する $\mathrm{DFA}$ よりもずっと小さいことやその機構がずっと理解しやすいことがある。有限オートマトンにおける非決定性はより強力な計算モデルにおける非決定性を理解するのに良い導入となる。なぜならば有限オートマトンは理解が特別に簡単なモデルだからである。

1.2.1　非決定的有限オートマトンの形式的定義

　非決定的有限オートマトンも決定的有限オートマトンにおけるものと同様に定義できる。いずれも状態、入力アルファベット、遷移関数、開始状態および許容状態の集合を有する。しかし、1つ本質的な面で相違がある。すなわち遷移関数の形態である。 $\mathrm{DFA}$ において、遷移関数は開始時点と入力文字を得て、次の状態を出力する。これに対して $\mathrm{NFA}$ では開始時点ならびに入力文字または空文字を受けて、想定し得る次の状態の集合を出力する。ついては追加的に記号を導入する必要がある。任意の集合 $Q$ に対して $Q$ の任意の部分集合の集合列を表すのに $\mathcal{P}(Q)$ を用いることとする。 $\mathcal{P}(Q)$ は $Q$ の冪集合と呼ばれる。任意のアルファベット $\mathit{\Sigma}$ に対して $\mathit{\Sigma}_{\varepsilon}$ で $\mathit{\Sigma}\cup\{\varepsilon\}$ を表すものとする。以上をもとに遷移関数の形式的な表記として $\delta:Q\times\mathit{\Sigma}_{\varepsilon}\rightarrow\mathcal{P}(Q)$ を考える。