計算理論（その02/X） - 「大人の教養・知識・気付き」を伸ばすブログ

はじめに

Introduction to the Theory of Computation

作者:Sipser, Michael
Course Technology Inc

Amazon

を参照しつつ計算理論を学んでいきます。

前回

power-of-awareness.com

はじめに
前回
1.　正規言語
- 1.1　有限オートマトン
  - 1.1.1　有限オートマトンの定義
  - 1.1.2　計算の定義
次回

1.　正規言語

　計算理論はまず「コンピュータとは何か」という問いから始まる。手許にあるノートPCなどのパソコンはコンピュータとしてはあまりに複雑すぎるため、理論的には計算モデル( $computational\ model$ )という理想的なコンピュータを用いる。科学で用いるモデルと同様に計算モデルはある面では正確である一方で、別の面では不正確である。したがって注目したい特徴に応じて異なる複数の計算モデルを扱うことにする。

1.1　有限オートマトン

　有限オートマトン( $\mathrm{finite\ automata}$ )は極度に限られたメモリしか持たないコンピュータに良いモデルである。現実における自動ドアのような単純な動作をモデル化するのに利用可能である。

図1　自動ドアの開閉を表す状態ダイアグラムと状態遷移表

この自動ドアの操作主は1ビットのメモリを持ち操作主が2つの状態のどちらにあるかを記録するコンピュータである。

　有限オートマタとそれに確率論で対応するマルコフ連鎖( $\mathrm{Markov\ chain}$ )は、データにあるパターンを認識しようとするときに有用な道具である。これらの道具は発話過程や最適特徴認識においても用いられる。マルコフ連鎖は金融市場における価格変化をモデル化し予測するのにさえも用いられる。
　有限オートマタを数学的な観点から見ることにする。

図2　3つの状態を持つ有限オートマトン $M_1$

　上のような有限オートマトンを考え、 $q_1$ を初期状態、 $q_2$ を受容(受理)状態とし、文字列 $\mathrm{1101}$ が入力されたとする。すると

初期状態 $q_1$ から開始する。
$\mathrm{1}$ を読み込み、 $q_1$ から $q_2$ へと遷移する。
$\mathrm{1}$ を読み込み、 $q_2$ から $q_2$ へと遷移する。
$\mathrm{0}$ を読み込み、 $q_2$ から $q_3$ へと遷移する。
$\mathrm{1}$ を読み込み、 $q_3$ から $q_2$ へと遷移する。
$M_1$ が入力の最後で受容(受理)状態 $q_2$ にいるため、受容(受理)する。

という動作をする。

1.1.1　有限オートマトンの定義

　このような具体的な例を受けて有限オートマトンを形式的に定義する。まず形式的な定義は厳密でなければならない。そのためにも想定し得る状態を明確にしなければならない。また形式的な定義は表記法を提供し、これにより考えたり考えたことを表現するのを明敏にする。厳密に記載し、すべての詳細を書き切らなければならない。

　有限オートマトンはいくつかの部分に分けられる。入力シンボルに応じて、ある状態から別の状態へと遷移する状態の集合およびその規則が存在する。受容(受理)された入力シンボルを表す入力アルファベットがある。初期状態があり、受容(受理)状態を表す集合が存在する。形式的な定義は、有限オートマトンはこうした5つの要素のリストである、すなわち状態集合、入力アルファベット、移動規則、初期状態および受容(受理)状態である。したがって有限オートマトンをこれら5つの要素を持つ5-タプルとして定義される。

　移動規則を表現するために、たびたび $\delta$ と書かれる遷移関数と呼ばれるものを用いる。もし有限オートマトンが入力シンボル $1$ で表される、ある状態 $x$ から状態 $y$ への矢印、それは $1$ を読み込んだときにもしオートマトンが状態 $x$ にいる場合を意味するが、を持つならば、そのとき状態 $y$ へと遷移する。これを $\delta(x,1)=y$ と書く。

定義1.1　有限オートマトン　それぞれの成分が

状態と呼ばれる有限集合 $Q$
文字列(アルファベット)と呼ばれる有限集合 $\mathit{\Sigma}$
遷移関数 $\delta:Q\times \mathit{\Sigma}\rightarrow Q$
初期状態 $q_0\in Q$
受容(受理)状態集合 $F\subset Q$

であるような5-タプル $\left(Q,\mathit{\Sigma},\delta,q_0,F\right)$ を有限オートマトンという。

例
　 $M_1=(Q,\mathit{\Sigma},\delta,q_1,F)$ と書かれる有限オートマトンを定義する。ここで

$Q=\{q_1,q_2,q_3\}$

$\mathit{\Sigma}=\{0,1\}$

$\delta$ は以下の表で与えられる。

　　　　　 $0$ $1$

　　 $q_1$ $q_1$ $q_2$

　　 $q_2$ $q_3$ $q_2$

　　 $q_3$ $q_2$ $q_2$

$q_1$ を初期状態とする

$F=\{q_2\}$

これは図2で与えたものの形式的な定義に他ならない。

　もし $A$ が機械 $M$ が受容(受理)するすべての文字列からなる集合であるならば、 $A$ は $M$ の機械語であるといい、 $L(M)=A$ と書く。このことを $M$ は $A$ を認識する( $recognize$ )、もしくは $M$ は $A$ を受容(受理)する( $accept$ )。受容(受理)という言葉は文字列を受容(受理)する機械や言語を受容(受理)する機械を扱うときに異なる意味を有することから、認識する( $recognize$ )を用いる方が望ましい。
　機械は複数の文字列を受容(受理)し得るものの、常にただ1つの言語のみを認識する。もし機械がいかなる文字列をも受容(受理)しない場合、空言語 $\emptyset$ を充てる。

1.1.2　計算の定義

　ここまでで有限オートマトンに、非形式的には状態ダイアグラムとして、形式的には5-タプルとして言及してきた。次にオートマトンにおける計算について同様のことを行なうことにする。

定義1.2　文字列の受容(受理)　 $M=(Q,\mathit{\Sigma},\delta,q_0,F)$ を有限オートマトンとし、 $w=w_1w_2\cdots w_n$ を各 $w_i$ がアルファベット $\mathit{\Sigma}$ に属する文字列だとする。このとき、もし $Q$ に属する状態の列 $r_1,\cdots,r_n$ が存在し、3つの条件

$r_0=q_0$
$i=0,1,\cdots,n-1$ に対して $\delta(r_i,w_{i+1})=r_{i+1}$
$r_n\in F$

を満たすならば、 $M$ は $w$ を受容(受理)するという。

　条件1 $r_0=q_0$ は、機械が初期状態から始まることを主張する。条件2 $i=0,1,\cdots,n-1$ に対して $\delta(r_i,w_{i+1})=r_{i+1}$ は、機械が遷移関数に従って状態から状態へと遷移することを意味する。そして条件3 $r_n\in F$ は受容(受理)状態で終わるのであれば、その入力を受容(受理)することを意味する。もし機械語 $A=\{w|Mはwを受容(受理)する\}$ ならば、 $M$ は言語 $A$ を受容(受理)するという。

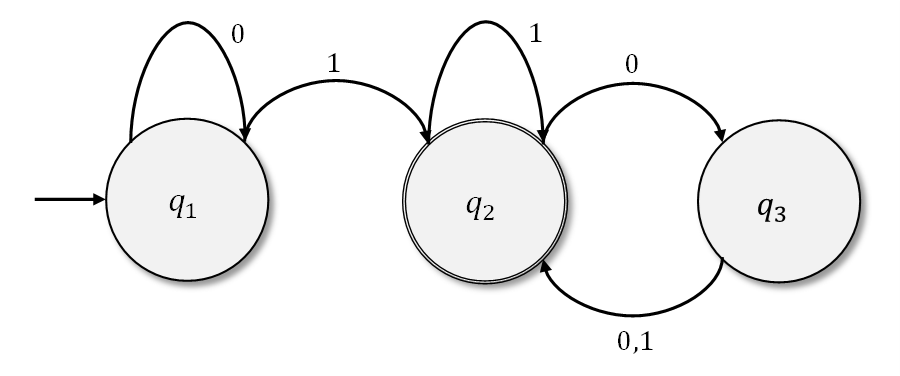
定義1.3　正規言語　ある言語は、その言語を認識する有限オートマトンが存在するならば、正規言語(正則言語)と呼ばれる。

　 $M=(Q,\mathit{\Sigma},\delta,q_0,F)$ と書かれる有限オートマトンを定義する。ここで

$Q=\{q_0,q_1,q_2\}$

$\mathit{\Sigma}=\{<\mathrm{RESET}>0,1,2\}$ ( $<\mathrm{RESET}>$ を1つの状態とする。)

$\delta$ は以下の表で与えられる。

　　　　　 $<\mathrm{RESET}>$ $0$ $1$ $2$

　　 $q_0$ $q_0$ $q_0$ $q_1$ $q_2$

　　 $q_1$ $q_0$ $q_1$ $q_2$ $q_0$

　　 $q_2$ $q_0$ $q_2$ $q_0$ $q_1$

$q_0$ を初期状態とする

$F=\{q_0\}$

とする。
　文字列 $w=\{\mathrm{10}<\mathrm{RESET}>\mathrm{22}<\mathrm{RESET}>\mathrm{012}\}$ とすれば、 $M_5$ は形式的な計算の定義に則り $w$ を認識する。なぜならば $w$ を計算しているときの状態列は、
$\begin{aligned} q_0,q_1,q_1,q_0,q_2,q_1,q_0,q_0,q_1,q_0 \end{aligned}$
であり、3つの条件を満たす。
　 $M$ の言語は
$\begin{aligned} L(M)=&\left\{w|<\mathrm{RESET}>は例外的にカウントを0とするものとして\right.\\&\left.wの文字数が3で割り切れる\right\} \end{aligned}$
である。 $M$ はこの言語を認識するため、これは正規言語である。