Juliaを基礎からゆっくりと（その16/18）

　や、言語関係など覚えたいもの、覚えるべきものはたくさんある一方で、注目が集まっているから、やってみたい。ということでプログラミング言語としてのを学んでいく。

1から始める Juliaプログラミング

前回

power-of-awareness.com

4.　Juliaの高速化

4.1　プロファイリング

　プログラムを高速化するには、コード処理にかかる時間を計測するプロファイリングが肝要である。プログラムの中で実行に特に時間のかかっている部分をボトルネックという。プロファイリングを行なうことでボトルネックを効率的に発見することが、高速化に向けた第一歩である。

4.1.4　メモリ割り当てのプロファイリング

　メモリ割り当てのプロファイリングも重要である。メモリをプロファイリングする場合、関数のコンパイルにもメモリを必要とするため一度関数を呼び出してコンパイルを行ない、メモリの使用量に関する記録をリセットして再度同じ関数を呼び出して計測する。

function diffuse(W₀, A; t = 100)
    P = sum(A, dims = 2) .\ A
    W = copy(W₀)
    for _ in 1:t
        W = W * P
    end
    return W
end

# プロファイリングの準備
N = 1000
A = rand(N, N)
A += A'
W₀ = zeros(N, N)
for i in 1:N W₀[i,1] = 1 end
diffuse(W₀, A)

# プロファイリング
using Profile
Profile.clear_malloc_data() # 記録のリセット
diffuse(W₀, A)

4.2　最適化しやすいコード

　の処理系では、コンパイラは動的にコンパイルするため、何気ないコードが想定外のパフォーマンス低下をもたらす可能性がある。あ

4.2.1　コードの書き方による性能差

　以下の例は、のコンパイラ能力を発揮できていないものである。

### 悪い書き方
using Random
Random.seed!(1234)

xs = rand(10000)
@time for i in 2:length(xs)
    j = i
    while j > 1 && xs[j-1] > xs[j]
        xs[j-1], xs[j] = xs[j], xs[j-1]
        j -= 1
    end
end

@assert issorted(xs)

# 良い書き方
using Random
Random.seed!(1234)

function isort!(xs)
    for i in 2:length(xs)
        j = i
        while j > 1 && xs[j-1] > xs[j]
            xs[j-1], xs[j] = xs[j], xs[j-1]
            j -= 1
        end
    end
    return xs
end

xs = rand(10000)
@time isort!(xs)
@assert issorted(xs)

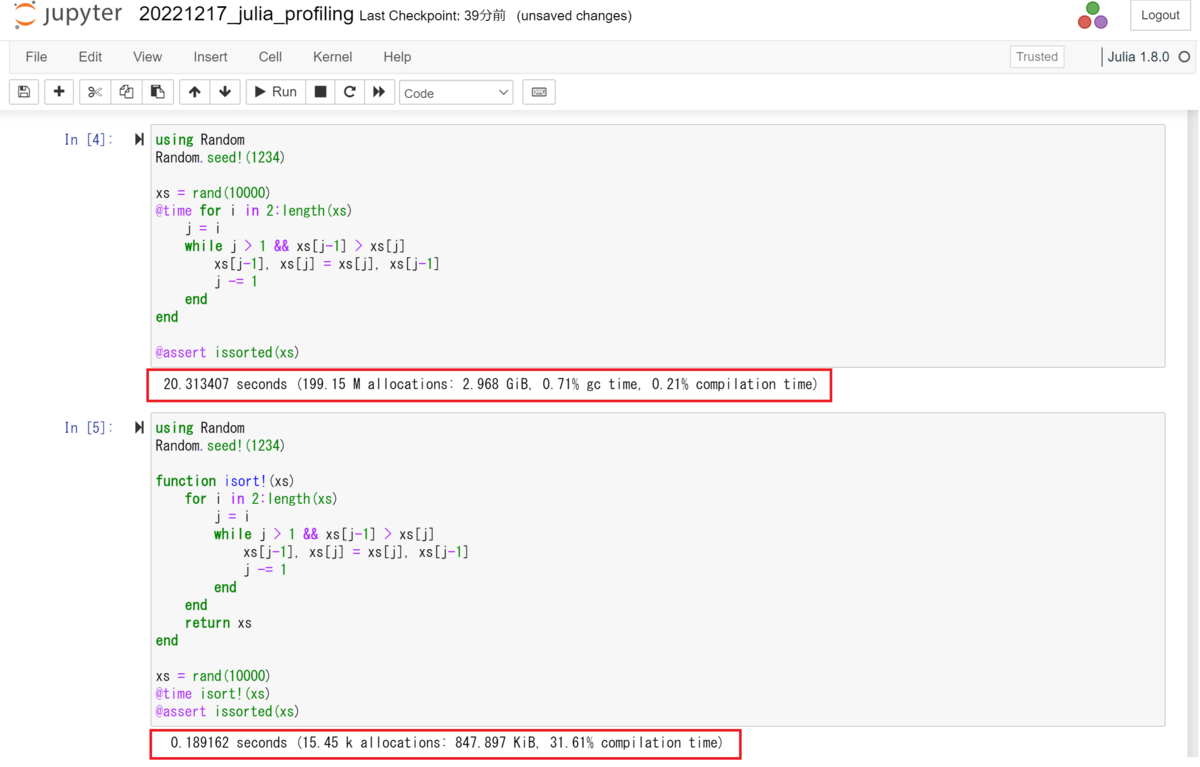
　前者では型が不明なグローバル変数（）を参照する一方で、後者では型が決定できるローカル変数を参照している。

4.2.2　コンパイラの概要

　で最適化しやすいコードを書くためには、コンパイラの特徴を踏まえておくべきである。

• のコンパイラは、のソースコードを構文解析して構文木に変換した後、低レベルなコードへと変換する。
• 次にコンパイラは低レベルのコードに対して型推論を行なう。型推論は、コード内の変数等の型を推定する仕組みである。

function func_sum(xs)
    s = 0
    for i in 1:length(xs)
        s += xs[i]
    end
    return s
end

print(@code_lowered func_sum([1,2,3])) # 低レベルコード
print(@code_typed func_sum([1,2,3]))   # 型推論の結果
print(@code_llvm func_sum([1,2,3]))    # LLVM中間表現
print(@code_native func_sum([1,2,3]))  # 機械語表現

4.2.3　型に不確実性のあるコード

　のコンパイラは実行時に型推論を行なう。最適化が上手く機能するように、型推論器が型を正確に推論できるように書くことが速いコードを書くコツの1つである。
　他方では動的プログラミング言語であるため、型が一意に定まらないプログラムを書くこともできる。たとえば

rand() < 0.3 ? 0 : 1.0

は確率で型を、で型を与える。
　他にも以下のようなコードで、不確実性が残る。以下は常微分方程式

を4次の-法で数値的に解く方法である(はそれぞれ反復回数と刻み幅を与えるパラメータである。)。

function solve_ode(f, t₀, y₀, n, h)
    t, y =  t₀, y₀
    
    for _ in 1:n
        k₁ = f(t          ,y               )
        k₂ = f(t + h * 0.5,y + k₁ * 0.5 * h)
        k₃ = f(t+ h * 0.5,y + k₂ * 0.5 * h)
        k₄ = f(t + h      ,y + k₃       * h)
        t += h
        y += h * (k₁ + 2k₂ + 2k₃ + k₄) / 6
    end
    return t, y
end

これは初期値の型がにもにもなり得る点で型が曖昧である。

　型の不確実性があるかをチェックするには、@_を用いるとよい。更に@_を用いると、型に不確実性の残る部分を強調してくれる。

　型の不確実性問題を解決するには、

• 引数の型を限定する（関数を定義する際に型を指定する）
• 関数内で型を特定の型に正規化する

次回

power-of-awareness.com