「大人の教養・知識・気付き」を伸ばすブログ

一流の大人（ビジネスマン、政治家、リーダー…）として知っておきたい、教養・社会動向を意外なところから取り上げ学ぶことで“気付く力”を伸ばすブログです。データ分析・語学に力点を置いています。　→諸事情により、2023年4月～8月くらいまで更新を不定期にします。

MENU

Rによるデータサイエンス（21/21）

R

　Rについて

Rによるデータサイエンス(第2版):データ解析の基礎から最新手法まで

Rによるデータサイエンス(第2版):データ解析の基礎から最新手法まで

Amazon

をベースに学んでいく。
　今回は生存分析（PP.296-311）を扱う。

前回

https://power-of-awareness.com/entry/2022/08/17/120000power-of-awareness.com

22.　生存分析

　生存分析は事象が起きるまでの時間とその事象との間の関係に焦点を当てる手法である。応用先には倒産、機械の故障、疾患や死亡の分析があり、これらを総称して広義の死亡と見なすことにする。
　生存時間に関する試験・観測では、治療の中止や転院などにより、データが脱落する場合がある。また研究の終了時点では死亡に関するデータが入手できないことが起こり得る。このようなことを打ち切りが生じたという。
　生存時間Tを確率変数として、以下のように確率密度関数f(x)を定義する：


\begin{aligned} f(t)=\begin{cases} \displaystyle{\lim_{\Delta t\rightarrow0}\frac{P\left\{t\lt T\lt t+\Delta t\right\}}{\Delta t}},&連続のとき,\\ P(T=t),&不連続のとき \end{cases} \end{aligned}


である。ここでP(\cdot)は生存確率である。累積確率分布関数をF(t)で表すと


\begin{aligned} F(t)=\begin{cases} \displaystyle{\int_0^t f(s)}ds,&連続のとき\\ \displaystyle{\sum_{s=0}^{t}}f(s),&不連続のとき \end{cases} \end{aligned}


となり、イベントが時点tまで生起していない確率である生存関数S(t)は


\begin{aligned} S(t)=P\left\{T\gt t\right\}=1-P\{T\leq t\}=1-F(t) \end{aligned}


で表される。イベントがある時点tまでに生起していないという条件の下で、その直後の瞬間にイベントが生起する(瞬間死亡率を表す)ハザード関数h(t)は


\begin{aligned} h(t)=\begin{cases} \displaystyle{\lim_{\Delta t\rightarrow0}\frac{P\{t\leq T\lt t+\Delta t|T\geq t\}}{\Delta t}}=\displaystyle{\frac{f(t)}{S(t)}},&連続のとき\\ P(T=t|T\geq t)=\displaystyle{\frac{f(t)}{S(t-1)}},&不連続のとき \end{cases} \end{aligned}


となる。生存関数S(t)とハザード関数h(t)および累積ハザード関数H(t)との関係は


\begin{aligned} H(t)=\displaystyle{\int_0^t h(t)dt}=\log S(t) \end{aligned}


で表すことができる。
　生存分析は生存時間に影響を与える時間以外の共変量がパラメータとしてモデルに導入されているか否か、生存時間の分布形に特定の確率分布を仮定するか否かによって

　　　 ノンパラメトリックモデル 共変数を導入しない、分布を仮定しない。
　　　 セミパラメトリックモデル 共変数を導入する、分布を仮定しない。
　　　 パラメトリックモデル 共変数を導入する、分布を仮定する。

と分類できる。

22.1　ノンパラメトリックモデル

　ノンパラメトリックな生存時間推定には

  • 経験分布による推定法
  • ハザード関数による推定法

の2つがある。

22.1.1　経験分布による推定

　打ち切りの無い完全データであれば、経験分布\hat{F}(t)を用いて


\begin{aligned} \hat{S}(t)=1-\hat{F}(t) \end{aligned}


で推定できる。

22.1.2　ハザード関数による推定

　\mathrm{Kaplan}-\mathrm{Meier}推定量


\begin{aligned} \hat{S}(t)=\displaystyle{\prod_{t_i\lt t}\left(1-\displaystyle{\frac{d_i}{r_i}}\right)} \end{aligned}


を用いて(d_iは時点t_iにおける死亡数、r_iは時点t_iの直前までイベントが生じる可能性のある観察対象者の数である。)、累積ハザード関数およびその推定量はそれぞれ


\begin{aligned} H(t)=-\log S(t),\ \hat{H}(t)=-\log\hat{S}(t) \end{aligned}


である。\mathrm{Kaplan}-\mathrm{Meier}推定量から求めたハザード関数の推定量


\begin{aligned} \hat{H}(t)=\displaystyle{\sum_{t_i\leq t}\frac{d_i}{r_i} } \end{aligned}


を\mathrm{Nelson}推定量と呼ばれる。また\mathrm{Nelson}推定量を修正した


\begin{aligned} \hat{H}(t)=\displaystyle{\sum_{t_i\leq t}\sum_{k=0}^{d_i-1}\frac{1}{r_i-k}}, \hat{S}(t)=\exp\left(-\hat{H}(t)\right) \end{aligned}


を\mathrm{Fleming}-\mathrm{Harrington}推定量と呼ぶ。

library("MASS")
library("survival")
library("survminer")

### 生存時間データオブジェクトを生成
Surv(gehan$time,gehan$cens)


### survfitを適用
ge_sf <- survfit(formula = formula(Surv(time, cens)~treat), data = gehan)


ggsurvplot(ge_sf,conf.int=T, conf.int.style = "ribbon", conf.int.alpha = 0.5,
           xlab = "生存時間",
           ylab = "生存確率",
           legend = "top",
           legend.title = "凡例",
           legend.labs=c("6-MP投与群","対照群"))

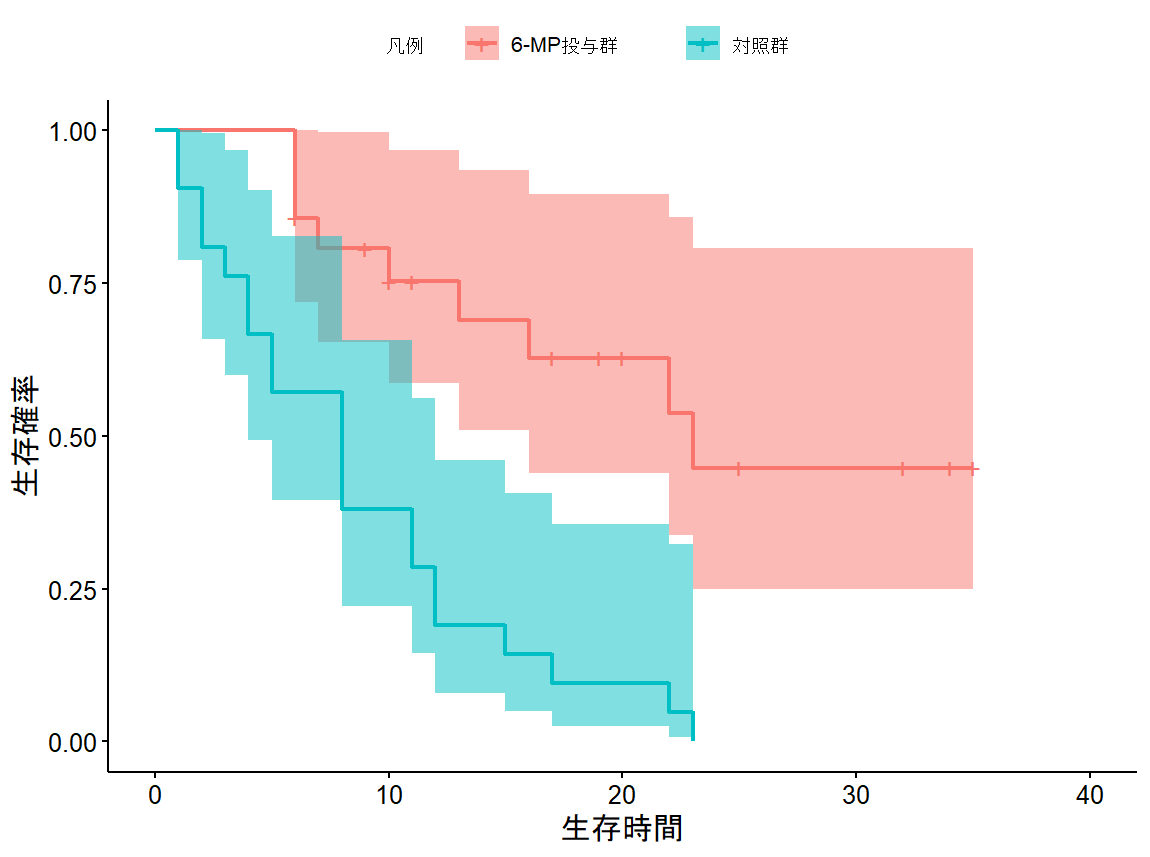
22.1.1　生存関数の検定

　2群以上の観測値が得られたときに、群ごとの生存曲線間の差の有意性を検定する場合がある。頻用されるのは\mathrm{log}-\mathrm{rank}検定法で、群ごとにイベントありと無しとを集計したクロス表のカイ二乗値の推定値を検定統計量とするものである。
　

survdiff(Surv(time)~treat,data=gehan, rho = 0) # p =0.003なので帰無仮説を棄却

22.2　セミパラメトリックモデル

　生存解析に用いるセミパラメトリックモデルとして\mathrm{Cox}比例ハザードモデルがある。ハザード関数h_1(t),h_2(t)に対して、すべて可能なt\gt0に対しh_1(t)=ch_2(t)が成り立つとき、h_1とh_2は比例するという。共変量\boldsymbol{x}={}^{t}(x_1,\cdots,x_m)を持つハザード関数h(t|\boldsymbol{x})とし、\boldsymbol{x}を変数とする関数r(\boldsymbol{x})とあるハザード関数h_0(t)を用いて、すべてのt\gt0と\boldsymbol{x}について


\begin{aligned} h(t|\boldsymbol{x})=h_0(t)\exp({}^{t}\boldsymbol{\beta}\boldsymbol{x})=h_0(t)\exp\left(\displaystyle{\sum_{i=1}^{m}\beta_i x_i}\right) \end{aligned}


とするモデルを\mathrm{Cox}比例ハザードモデルという。
　\boldsymbol{\beta}={}^{t}(\beta_1,\cdots,\beta_m)は条件付き確率の部分尤度


\begin{aligned} PL(\boldsymbol{\beta})=\displaystyle{\prod_{j=1}^{M}\frac{\exp({}^{t}\boldsymbol{\beta}\boldsymbol{X}_k)}{\displaystyle{\sum_{k\in R(t_j)}\exp({}^{t}\boldsymbol{\beta}\boldsymbol{X}_k)}}} \end{aligned}


を最大化することで推定できる。ここでj=1,2,\cdots,Mはイベント数、t_jはイベント時点、R(t_j)各時点におけるリスクの集合である。

22.2.1　Cox比例ハザードモデルの推定

　\mathrm{survival}パッケージには\mathrm{Cox}比例ハザードモデルの推定を行なう\mathrm{coxph}()関数がある。

#############################
### Cox比例ハザードモデル ###
#############################
library("survival")

cox_kidney <- coxph(formula = formula(Surv(time,status)~sex+disease),data = kidney)
summary(cox_kidney)

kidney_fit <- survfit(cox_kidney)
summary(kidney_fit)

plot(kidney_fit)
22.2.2　残差分析

　\mathrm{Cox}比例ハザードモデルでは、打切りデータが存在することもあり、一般線形回帰モデルの残差分析ほど単純ではない。そのためマルチンゲール残差など様々な残差が提案されている。
　残差は\mathrm{residuals.coxph}で呼び出すことができる。

scatter.smooth(residuals(cox_kidney))
22.2.3　ハザードの比例性分析

　\mathrm{cox.zph}()関数を用いることで、シェーンフィールド残差を用いて、\boldsymbol{\beta}(t)=\boldsymbol{\beta}+\theta g(t)における仮説H_0:\theta=0の検定に必要な関数を返す。

zph_kidney <- cox.zph(cox_kidney)

zph_kidney

plot(zph_kidney)


スプライン平滑化曲線の傾向に、時間に伴う明らかな変化パターンが見られなければ、比例ハザードの仮定に問題が無いと言われる。
個別の変数に比例ハザードの仮定が満たされていない場合には、変数の交互作用をモデルに導入するような試みが必要になる。

22.3　パラメトリックモデル

　パラメトリックモデルを導入する場合、生存時間の確率分布を仮定するこになるため、応用範囲が限定される。生存時間モデルには、指数分布や\mathrm{Weibull}分布、対数正規分布、対数ロジスティック分布などが用いられる。

survreg(formula = formula(Surv(time, status) ~ sex + disease), kidney, dist = "lognormal")

補足　スペック情報

エディション Windows 10 Home
バージョン 20H2
プロセッサ Intel(R) Core(TM) i5-1035G4 CPU @ 1.10GHz 1.50 GHz
実装 RAM 8.00 GB
システムの種類 64 ビット オペレーティング システム、x64 ベース プロセッサ
R　バージョン 4.1.3 (March, 2022)
RStudio　バージョン 2022.02.2 Build 485
プライバシーポリシー お問い合わせ