本気で学ぶ統計学(25/31) - 「大人の教養・知識・気付き」を伸ばすブログ

　統計学を真剣に学ぶ人のために、個人的にまとめているノートを公開する。
　底本として

新装改訂版現代数理統計学

作者:彰通, 竹村
学術図書出版社

Amazon

を用いる。

前回
8.　統計的仮説検定
- 8.3　良い検定手法の定義：一様最強力検定・不偏検定・尤度比検定
  - 8.3.4　尤度比検定
- 8.4　仮説検定における精度と標本サイズの関係
参考文献

前回

power-of-awareness.com

8.　統計的仮説検定

8.3　良い検定手法の定義：一様最強力検定・不偏検定・尤度比検定

　「“良い”検定」とは何か。伝統的な検定手法に立脚すれば、前述のとおり第1種の過誤を犯す確率を有意水準 $\alpha$ に抑えたうえで対立仮説のもとでの検出力を最大にする（第2種の過誤を犯す確率を最小化する）ものである。こうしたものを与える条件を具体的に考えるために有用な概念が「（一様）最強力検定」「不偏検定」「尤度比検定」である。
　「（一様）最強力検定」とは検出力の高い検定の方が“良い”検定であるという、言ってみれば当たり前の条件を明言化するための考えである。しかしそれはすべての検定において常に存在するというわけではない。そこでもし（一様）最強力検定が存在しないのであれば、（一様）最強力検定が存在するように検定族を制約する「条件」を加えることを考えればよく、そのための条件が検定における「不偏性」である。

8.3.4　尤度比検定

　ここまでは $\mathrm{Neyman}$ - $\mathrm{Pearson}$ の補題という前提で尤度比を導入したが、これはその前提が無くとも考えることができる。
　確率変数 $X=(X_1,\cdots,X_n)$ *1に対して $f_n(x;\theta)=\displaystyle{\prod_{i=1}^{n}f(x_i;\theta)},\theta\in\Theta$ を同時密度関数とするとき、一般的な仮説検定問題

$\begin{aligned} H_0:\theta\in\Theta_0\ \ \mathrm{v.s.}\ \ H_1:\theta\in\Theta_1 \end{aligned}$

を考える。このとき

$\begin{aligned} L:=\displaystyle{\frac{\displaystyle{\sup_{\theta\in\Theta_1}f_n(x,\theta)}}{\displaystyle{\sup_{\theta\in\Theta_0}f_n(x,\theta)}}} \end{aligned}$

を尤度比(統計量)という。さらにこの対数を取った $l=\log L$ を対数尤度比という。帰無仮説および対立仮説の双方が単純仮説の場合、尤度比検定統計量は $\mathrm{Neyman}$ - $\mathrm{Pearson}$ の補題に現れた尤度比に一致する。
　帰無仮説のもとでの最尤推定量 $\tilde{\theta}:=\displaystyle{\mathrm{arg}\sup_{\theta\in\Theta_0}f_n (x,\theta)}$ および対立仮説のもとでの最尤推定量 $\hat{\theta}:=\displaystyle{\mathrm{arg}\sup_{\theta\in\Theta_1}f_n(x,\theta)}$ としたときに棄却域を

$\begin{aligned} &\begin{cases} L=\displaystyle{\frac{f_n(x,\hat{\theta})}{f_n(x,\tilde{\theta})}}\gt c\Rightarrow帰無仮説を棄却する,\\ L=\displaystyle{\frac{f_n(x,\hat{\theta})}{f_n(x,\tilde{\theta})}}\leq c\Rightarrow帰無仮説を受容する, \end{cases}\\ &c\in R\ \ \mathrm{s.t.}\ \ \displaystyle{\sup_{\theta\in\Theta_0}P_{\theta}\left\{L\lt c\right\}}=\alpha,0\lt\alpha\lt1 \end{aligned}$

としたものを尤度比検定と呼ぶ。
　尤度比検定は複合仮説検定問題を単純仮説問題

$\begin{aligned} H_0:\theta\in\tilde{\Theta}\ \ \mathrm{v.s.}\ \ H_1:\theta\in\hat{\Theta} \end{aligned}$

に置き換えて $\mathrm{Neyman}$ - $\mathrm{Pearson}$ の補題を適用した形式の検定方式である。そこから推察できるように、尤度比検定は、

	(1)	尤度比検定 $\delta_L(\boldsymbol{x})$ の検出力 $\beta_{\delta_L}(\theta)$ は各 $\theta\in\Theta_1$ について $n\rightarrow\infty$ のとき $1$ に収束するという一致性を持つ。
	(2)	$X_1,\cdots,X_n$ が独立に得られているならば、尤度比検定は $n$ が十分に大きければ漸近的に最大の検出力を持つという漸近有効性を持つ。

といった性質を持つ“良い”検定であると言える。
　ただし具体的な問題において棄却限界 $c$ を正確に求めるのが困難な場合が多い。それでも、標本サイズ $n$ が十分に大きければ、その値がカイ二乗分布に近似的に従うことが知られており、そこから近似値を求めることは可能である。

尤度比検定における棄却限界の漸近分布　仮説検定問題

$\begin{aligned} H_0:\theta\in\Theta_0\ \ \mathrm{v.s.}\ \ H_1:\theta\in\Theta_1 \end{aligned}$

における尤度比

$\begin{aligned} L=\displaystyle{\frac{\displaystyle{\sup_{\theta\in\Theta_1}f_n(x,\theta)}}{\displaystyle{\sup_{\theta\in\Theta_0}f_n(x,\theta)}}} \end{aligned}$

に対して

$\begin{aligned} {}^{\forall}z\in(0,\infty)\left(\displaystyle{\lim_{n\rightarrow\infty}P_{\theta}\left\{-2\log L\leq z\right\}}=\displaystyle{\int_{0}^{z} g(t)}td \right) \end{aligned}$

である。ここで $g(t)$ は自由度 $q$ のカイ二乗分布の確率密度で $q$ は帰無仮説における母数空間 $\Theta_0$ の次元である。

すなわち、仮説検定

$\begin{aligned} H_0:\theta\in\Theta_0\ \ \mathrm{v.s.}\ \ H_1:\theta\in\Theta_1 \end{aligned}$

において有意水準 $\alpha$ の尤度比検定を考えると、自由度 $q$ のカイ二乗分布の上側 $100\alpha$ %点を $\chi^2_{\alpha}(q)$ とすれば、

$\begin{aligned} 2l=2\log L\gt\chi^2_{\alpha}(q) \end{aligned}$

を棄却域とすることで、漸近的に有意水準 $\alpha$ を得ることができる。このように、尤度比検定は点推定論における最尤推定のように汎用性に優れる点が利点である。

8.4　仮説検定における精度と標本サイズの関係

　検出力関数 $\beta_{\delta}(\theta):=E_{\theta}\left[\delta(X_1,\cdots,X_n)\right]=P_{\theta}\left\{\delta(X_1,\cdots,X_n)=1\right\}$ は当然ながら検定関数 $\delta$ に依存するが、標本サイズである $n$ にも依存する。すなわち、検定関数 $\delta$ の検出力を $\beta_{\delta}$ とすれば第2種の誤りを犯す確率は $1-\beta_{\delta}$ であることに注意すれば、

	(1)	帰無仮説は限定的である2から、第1種の誤りを犯す確率(有意水準) $\alpha$ は一意に定まる3。
	(2)	対立仮説は様々な母数などが変化するため、第2種の誤りを犯す確率 $1-\beta_{\delta}$ は母数などに応じ変化する。
	(3)	第1種の誤りを犯す確率(有意水準) $\alpha$ を小さく設定しても第2種の誤りを犯す確率 $1-\beta_{\delta}$ は非常に大きな値になり得る。
	(4)	第1種の誤りを犯す確率(有意水準) $\alpha$ を大きくすれば第2種の誤りを犯す確率 $1-\beta_{\delta}$ は小さくなる。
	(5)	標本サイズ $n$ が大きくなれば第2種の誤りを犯す確率 $1-\beta_{\delta}$ は小さくなる。

が成り立つ。
　 $1-\beta_{\delta}\gt0$ であるため、帰無仮説 $H_0$ を可能な限り保障するには検出力を大きくしなければならない。とはいえ標本サイズを無制限に増大させることは困難である。そこで「検定対象となる母数に水準 $\Delta_0$ 以上の差（ないし比）がある場合には高い検出力を保障できるようにしたい」のであり、そうした「高い検出力を得るために必要な標本サイズはどの程度なのか」を知るように問題を考えればよい。

例：母平均の両側検定における検出力
　正規分布 $N(\mu,1^2)$ に独立にしたがう確率変数の標本 $X_1,\cdots,X_n$ に対して、有意水準 $\alpha$ の仮説検定
$\begin{aligned} H_0:\mu=\mu_0\ \ \mathrm{v.s.}\ \ H_1:\mu\neq\mu_0 \end{aligned}$
を考える。
　このとき検定統計量
$\begin{aligned} U_0=\displaystyle{\frac{\bar{X}-\mu_0}{\displaystyle{\frac{\sigma}{\sqrt{n}}}}}=\displaystyle{\frac{\bar{X}-\mu_0}{\displaystyle{\frac{1}{\sqrt{n}}}}}=\sqrt{n}(\bar{X}-\mu_0) \end{aligned}$
は標準正規分布に従う。したがって $z_{\frac{\alpha}{2}}$ を標準正規分布の片側 $100\alpha$ %点だとして
$\begin{aligned} \alpha=P\left\{|U_0|\geq z_{\frac{\alpha}{2}}\right\}=P\left\{U_0\leq-z_{\frac{\alpha}{2}}\right\}+P\left\{U_0\geq z_{\frac{\alpha}{2}}\right\} \end{aligned}$
である。
　次に検出力 $\beta_{\delta}$ は、対立仮説 $\mu\neq\mu_0$ の下で
$\begin{aligned} \beta_{\delta}=&P\{|U_0|\geq z_{\frac{\alpha}{2}}\}\\ =&P\left\{\sqrt{n}(\bar{X}-\mu_0)\leq-z_{\frac{\alpha}{2}}\right\}+P\left\{\sqrt{n}(\bar{X}-\mu_0)\geq z_{\frac{\alpha}{2}}\right\}\\ =&P\left\{\sqrt{n}\{(\bar{X}-\mu)+(\mu-\mu_0)\}\leq-z_{\frac{\alpha}{2}}\right\}\\ &+P\left\{\sqrt{n}\{(\bar{X}-\mu)+(\mu-\mu_0)\}\geq z_{\frac{\alpha}{2}}\right\}\\ =&P\left\{\sqrt{n}(\bar{X}-\mu)\leq-z_{\frac{\alpha}{2}}-\sqrt{n}(\mu-\mu_0)\right\}\\ &+P\left\{\sqrt{n}(\bar{X}-\mu)\geq z_{\frac{\alpha}{2}}-\sqrt{n}(\mu-\mu_0)\right\}\\ \end{aligned}$
が成り立つ。 $\Delta=\mu-\mu_0$ とおけば、検出力 $\beta_{\delta}$ は標本サイズ $n$ および $\Delta$ に依存して決まることが分かる。
　 $\Delta$ は $\mu$ が未知であるから*4、 $\Delta$ を機械的に計算することはできない。そこで以下の2つの考え方で $\Delta$ を定める手段が考えられる：
　帰無仮説の下での母平均の正規分布 $N(\mu_0,1)$ に従う母集団1と未知母数の正規分布 $N(\mu,1)$ に従う母集団2に対して、

　　 (1) 一方の母集団の $100p$ %がもう一方の母集団の $100p$ %より大きくなれば $H_0$ を棄却する。

　　 (2) 一方の母集団の $50$ %がもう一方の母集団の $100p$ %より大きくなれば $H_0$ を棄却する。

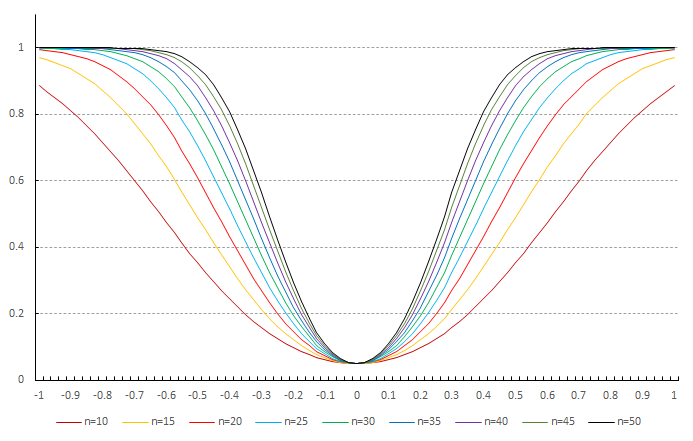
母平均の両側検定における標本サイズ別の検出力曲線

　　　　　　

　 $|\Delta|\geq\Delta_0\gt0$ を与えたときに高い検出力 $\beta_{\delta}(\mu)=\beta$ で $H_0$ を棄却したいとすれば、 $\sqrt{n}\Delta$ が非常に小さい場合を除けば
$\begin{aligned} \beta\approx P\left\{U_0\geq z_{\frac{\alpha}{2}}-\sqrt{n}\Delta\right\} \end{aligned}$
が成り立つから、 $\Delta=\Delta_0$ のときに
$\begin{aligned} z_{\frac{\alpha}{2}}-\sqrt{n}\Delta_0\approx z_{\beta} \end{aligned}$
であればよく、したがって標本サイズ $n$ は
$\begin{aligned} n\approx\left(\displaystyle{\frac{z_{\frac{\alpha}{2}}-z_{\beta}}{\Delta_0}}\right)^2 \end{aligned}$
とすればよい。

参考文献

Lehmann, E.L., Casella, George(1998), "Theory of Point Estimation, Second Edition", (Springer)
Lehmann, E.L., Romano, Joseph P.(2005), "Testing Statistical Hypotheses, Third Edition", (Springer)
Sturges, Herbert A.,(1926), "The Choice of a Class Interval", (Journal of the American Statistical Association, Vol. 21, No. 153 (Mar., 1926)), pp. 65-66
Wald, A.,(1950), "Statistical Decision Functions", John Wiley and Sons, New York; Chapman and Hall, London
上田拓治（2009）「44の例題で学ぶ統計的検定と推定の解き方」(オーム社)
大田春外（2000）「はじめよう位相空間」(日本評論社)
小西貞則（2010）「多変量解析入門――線形から非線形へ――」(岩波書店)
小西貞則,北川源四郎（2004）「シリーズ予測と発見の科学2　情報量基準」(朝倉書店)
小西貞則,越智義道,大森裕浩（2008）「シリーズ予測と発見の科学5　計算統計学の方法」(朝倉書店)
佐和隆光（1979）「統計ライブラリー　回帰分析」(朝倉書店)
清水泰隆（2019）「統計学への確率論,その先へ　―ゼロからの速度論的理解と漸近理論への架け橋」(内田老鶴圃)
鈴木武, 山田作太郎（1996）「数理統計学　基礎から学ぶデータ解析」(内田老鶴圃)
竹内啓・編代表（1989）「統計学辞典」(東洋経済新報社)
竹村彰通（1991）「現代数理統計学」(創文社)
竹村彰通（2020）「新装改訂版　現代数理統計学」(学術図書出版社)
東京大学教養学部統計学教室編（1991）「基礎統計学Ⅰ　基礎統計学」(東京大学出版会)
東京大学教養学部統計学教室編（1994）「基礎統計学Ⅱ　人文・社会科学の統計学」(東京大学出版会)
東京大学教養学部統計学教室編（1992）「基礎統計学Ⅲ　自然科学の統計学」(東京大学出版会)
豊田秀樹（2020）「瀕死の統計学を救え！ ―有意性検定から「仮説が正しい確率」へ―」(朝倉書店)
永田靖（2003）「サンプルサイズの決め方」(朝倉書店)
柳川堯（2018）「Ｐ値　その正しい理解と適用」(近代科学社)

*1:各 $X_i$ は標本に相当し、ここで $i.i.d.$ と仮定する。

*2:たとえば母平均 $\mu=\mu_0$ という帰無仮説に対して $\mu\neq\mu_0$ という対立仮説を設定するように、帰無仮説は通常、母数空間の範囲を限定することがあるという意味である。

*3:ただし局外母数の影響で定まらない場合があることに注意されたい。

*4:さらに他の検定問題では母分散 $\sigma^2$ も未知であることが多い。

	(1)	一方の母集団の $100p$ %がもう一方の母集団の $100p$ %より大きくなれば $H_0$ を棄却する。
	(2)	一方の母集団の $50$ %がもう一方の母集団の $100p$ %より大きくなれば $H_0$ を棄却する。

前回

8. 統計的仮説検定

8.3 良い検定手法の定義：一様最強力検定・不偏検定・尤度比検定

8.3.4 尤度比検定

8.4 仮説検定における精度と標本サイズの関係

参考文献

8.　統計的仮説検定

8.3　良い検定手法の定義：一様最強力検定・不偏検定・尤度比検定

8.3.4　尤度比検定

8.4　仮説検定における精度と標本サイズの関係