Pythonで学ぶアルゴリズム（16/18） - 「大人の教養・知識・気付き」を伸ばすブログ

	モンテカルロ・アルゴリズム	乱数によっては結果が誤りになり得る乱択アルゴリズム。
	ラスベガス・アルゴリズム	乱数にかかわらず結果が常に正しい乱択アルゴリズム。

9.1.3　例：面接試験

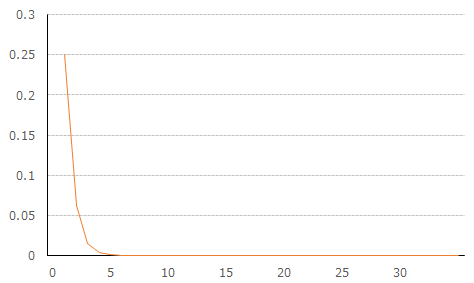
　二択で答えられる質問を何度も質問して面接相手を有望な人材かを選別することを考える。もし目の前に将来有望な人材が現われた場合、南海質問しても優れた回答が返ってくるためこの人物に対する評価は確信に変わり得る。普通の人材が優れた回答をする確率が $\displaystyle{\frac{1}{4}}$ だとすれば、何度も質問を重ねることで有望な人材をあ

9.2　数論

　数学の一分野である数論はアルゴリズムと相性が良い。数論の例に触れながら、アルゴリズムを紹介する。

9.2.1　合同式

　性数に話を限定し、さらに剰余を考えることにする。ある整数 $a,b$ についてある整数 $m$ で割ったときの剰余が等しいとき、

$\begin{aligned} a\equiv b\ \ \ \ (\mathrm{mod}\ m) \end{aligned}$

で表現する。これを合同式という。 $a$ と $b$ は $m$ を法として等しい(合同である)という。
　 $a\equiv b\ \ \ \ (\mathrm{mod}\ m)$ かつ $c\equiv d\ \ \ \ (\mathrm{mod}\ m)$ であるとき、

$\begin{aligned} a+c&\equiv b+d\ \ \ \ (\mathrm{mod}\ m)\\ a-c&\equiv b-d\ \ \ \ (\mathrm{mod}\ m)\\ ac&\equiv bd\ \ \ \ (\mathrm{mod}\ m)\\ ka&\equiv kb\ \ \ \ (\mathrm{mod}\ m),k\in\mathbb{Z} \end{aligned}$

が成り立つ。

9.2.2　フェルマーの小定理

　合同式を持ち出すと興味深い結果が得られる。

print('a\ta%3')

for a in range(10):
    print('{}\t{}'.format(a, a%3))

##############
m = 3

" 3も自分のスペースを用意して右に詰めるテンプレートを用意"
tmpl = '{:>3}' * 5
print(tmpl.format('a', 1, 2, 3, 4))
for a in range(m):
    print(tmpl.format(a, a % m, a**2 % m, a**3 % m, a**4 % m))
##############
def make_table(m):
    tmpl = '{:>5}' * (m+2)
    
    header = ['a']
    
    for i in range(1, m+2):
        header.append(i)
    print(tmpl.format(*header))
    for a in range(m):
        vals = [a]
        for i in range(1, m+2):
            vals.append(a**i % m)
        print(tmpl.format(*vals))

make_table(5)

　すなわち $a,p\in\mathbb{N}$ について

$\begin{aligned} a^{p-1}\equiv 1\ \ (\mathrm{mod}\ p) \end{aligned}$

が成り立つ。これを $\mathrm{Fermat}$ の小定理という。

9.2.3　冪乗と余り

　一般に $a^k,a\in\mathbb{N}$ を素数とは限らない $m\in\mathbb{N}$ で割った余りを計算したいとする。 $k$ が非常に大きいとまともには計算できない。そこでこれを効率的に解くべく繰り返し二乗法を用いる。
　たとえば $7^{43}$ を $123$ で割った余りを求めたいとする。ここで $43$ を二進数展開する。すなわち

$\begin{aligned} 43&=1\times2^5+0\times2^4+1\times2^3+0\times2^2+1\times2^1+1\times2^0\\ &=32+0+8+0+2+1 \end{aligned}$

である。したがって

$\begin{aligned} 7^{43}=7^{32}\times7^{8}\times7^{2}\times7^{1} \end{aligned}$

を得る。ここに $\mathrm{Fermat}$ の小定理を用いれば

$7^1$	$=$	$7$	$\equiv$	$7\ (\mathrm{mod}\ 123)$
$7^2$	$=$	$49$	$\equiv$	$49\ (\mathrm{mod}\ 123)$
$7^4$	$=$	$49^2$	$\equiv$	$64\ (\mathrm{mod}\ 123)$
$7^8$	$=$	$64^2$	$\equiv$	$37\ (\mathrm{mod}\ 123)$
$7^{16}$	$=$	$37^2$	$\equiv$	$16\ (\mathrm{mod}\ 123)$
$7^{32}$	$=$	$16^2$	$\equiv$	$10\ (\mathrm{mod}\ 123)$

となるから、

$\begin{aligned} 7^{43}&=7^{32}\times7^{8}\times7^{2}\times7^{1}\\ &\equiv10\times37\times49\times7\equiv97\ (\mathrm{mod}\ 123) \end{aligned}$

を得る。以上をアルゴリズムに落とし込むことで効率的に余りを求めることができる：

入力を $a,k,m$ とする。

(1) $b=1$ とする。

(2) $k$ の二進数表現を得て一番下の位から順に[texi]に格納し(3),(4)を繰り返す。

(3) $i=1$ ならば $ab$ を $m$ で割った余りを $b$ として更新する。そうでなければ(4)に移る。

(4) $a$ を二乗して $m$ で割った余りで $a$ を更新する。

(5) $b$ を出力する。

def a_m_mod_m(a, k, m):
    b = 1
    for i in reversed(bin(k)[2:]):
        if i=='1':
            b = a * b % m
        a = a**2 % m
    return b

a_m_mod_m(7, 43, 123)

(1)	$b=1$ とする。
(2)	$k$ の二進数表現を得て一番下の位から順に[texi]に格納し(3),(4)を繰り返す。
(3)	$i=1$ ならば $ab$ を $m$ で割った余りを $b$ として更新する。そうでなければ(4)に移る。
(4)	$a$ を二乗して $m$ で割った余りで $a$ を更新する。
(5)	$b$ を出力する。

前回

9. 乱択アルゴリズムと数論

9.1 アルゴリズムと乱数

9.1.1 乱択アルゴリズムの例：クイックソート

9.1.2 乱択アルゴリズムの種類

9.1.3 例：面接試験

9.2 数論

9.2.1 合同式

9.2.2 フェルマーの小定理

9.2.3 冪乗と余り

9.　乱択アルゴリズムと数論

9.1　アルゴリズムと乱数

9.1.1　乱択アルゴリズムの例：クイックソート

9.1.2　乱択アルゴリズムの種類

9.1.3　例：面接試験

9.2　数論

9.2.1　合同式

9.2.2　フェルマーの小定理

9.2.3　冪乗と余り