Rによるデータサイエンス（04/21） - 「大人の教養・知識・気付き」を伸ばすブログ

　Rについて

Rによるデータサイエンス(第2版):データ解析の基礎から最新手法まで

作者:金明哲
森北出版

Amazon

をベースに学んでいく。
　今回は主成分分析（PP.60-73）を扱う。

前回
5.　主成分分析
補足　スペック情報
次回

前回

power-of-awareness.com

5.　主成分分析

　多くの変数により記述された量的データの変数間にある相関関係を利用し、情報の損失を最小限に抑えつつ、もとの変数の線形結合で表される少数個の無相関な合成変数に縮約して分析する手法を主成分分析という。高次元データをより少数個の変数へ要約して次元圧縮を行い、1次元直線や2次元平面、3次元空間に射影してデータ構造を視覚的に把握するための手法として用いることができる*1。

5.1　主成分導出の過程

　一般次元の変数および一般の個数の標本に対する主成分導出の過程を説明しよう。各個体の特徴を捉える $p$ 個の変数を $\boldsymbol{X}=(X_1,\cdots,X_p)^{T}$ とする*2。この $p$ 個の変数に関して観測された $n$ 個の $p$ 次元データ $\boldsymbol{X}_1,\cdots,\boldsymbol{X}_n,\boldsymbol{X}_{i}=(X_{i1},\cdots,X_{ip})^{T},i=1,2,\cdots,n$ に基づいて標本分散共分散行列

$\begin{aligned} S&=(s_{jk})=\displaystyle{\frac{1}{n}\sum_{i=1}^{n}(\boldsymbol{X}_i-\bar{\boldsymbol{X}})(\boldsymbol{X}_i-\bar{\boldsymbol{X}})^{T}}\\ s_{jk}&=\displaystyle{\frac{1}{n}\sum_{i=1}^{n}(X_{ij}-\bar{X}_j)(X_{ik}-\bar{X}_{k})^{T}} \end{aligned}$

を計算する。ここで $\bar{\boldsymbol{X}}=(\bar{X}_1,\cdots,\bar{X}_p)^{T},\bar{X}_i=\displaystyle{\frac{1}{n}\sum_{j=1}^{n}X_{ji}}$ は $p$ 次元標本平均ベクトルである。
　まず $p$ 個の変数の線形結合で表される射影軸

$\begin{aligned} Y=\omega_1X_1+\cdots+\omega_pX_p=\boldsymbol{\omega}^{T}\boldsymbol{X} \end{aligned}$

上へ $n$ 個の $p$ 次元データを射影して、1次元データ $Y_i=\boldsymbol{\omega}^{T}\boldsymbol{X}_i,i=1,2,\cdots,n$ を得る。これらの平均 $\bar{y}$ は $\bar{Y}=\displaystyle{\frac{1}{n}\sum_{i=1}^{n}\boldsymbol{\omega}^{T}\boldsymbol{X}_i}=\boldsymbol{\omega}^{T}\bar{\boldsymbol{X}}$ であるから、その分散 $s_Y^2$ は

$\begin{aligned} s_Y^2=V[Y]&=\displaystyle{\frac{1}{n}\sum_{i=1}^{n}(Y_i-\bar{Y})^2}\\ &=\displaystyle{\frac{1}{n}\sum_{i=1}^{n}(\boldsymbol{\omega}^{T}\boldsymbol{X}_i-\boldsymbol{\omega}^{T}\bar{\boldsymbol{X}})^2}\\ &=\boldsymbol{\omega}^{T}\left\{\displaystyle{\frac{1}{n}\sum_{i=1}^{n}(\boldsymbol{X}_i-\bar{\boldsymbol{X}})^2}\right\}\boldsymbol{\omega}\\ &=\boldsymbol{\omega}^{T}S\boldsymbol{\omega} \end{aligned}$

で与えられる。したがって射影したデータの分散を最大にするような係数ベクトルは、標本分散共分散行列 $S$ の最も大きい固有値 $\lambda_1$ に対応する固有ベクトル $\boldsymbol{\omega}_1$ として与えられる。この $\boldsymbol{\omega}_1$ を係数とする射影軸 $Y_1=\boldsymbol{\omega}_1^{T}\boldsymbol{X}$ が第1主成分である。またその射影軸上での分散は最大固有値 $\lambda_1$ に等しい。
　第2主成分は第1主成分と直交するという条件の下で射影した $p$ 次元データの分散を最大にする軸として与えられ、これは分散共分散行列 $S$ の2番目の大きさの固有値 $\lambda_2$ に対応する固有ベクトル $\boldsymbol{\omega}_2$ を係数とする射影軸である。更に第3主成分は、第1、第2主成分と直交するという条件の下で射影した $p$ 次元データの分散を最大とする軸として定義される。
　この過程を順次繰り返すことによって理論上、もとの変数の線形結合で表される $p$ 個の主成分が導出される。以上の過程から明らかなように、主成分分析は標本分散共分散行列の固有値問題に帰着できる。

5.2　標本分散共分散行列の固有値問題と主成分

　観測された $n$ 個の $p$ 次元データに基づく標本分散共分散行列を $S$ とする。標本分散共分散行列は $p$ 次元対称行列である。そこで $S$ の固有方程式 $\mathrm{det}(S-\lambda I_p)=0$ の解として与えられる $p$ 個の固有値を

$\begin{aligned} \lambda_1\geq \lambda_2\geq\cdots\lambda_p\geq0 \end{aligned}$

とする。また各固有値に対応する、長さが $1$ になるように規格化した $p$ 次元固有ベクトルをそれぞれ

$\begin{aligned} \boldsymbol{\omega}_1=\begin{bmatrix}\omega_{11}\\\omega_{12}\\\vdots\\\omega_{1p}\end{bmatrix},\cdots,\boldsymbol{\omega}_p=\begin{bmatrix}\omega_{p1}\\\omega_{p2}\\\vdots\\\omega_{pp}\end{bmatrix} \end{aligned}$

とおく。これらの固有ベクトルは規格化と直交化、すなわち

$\begin{aligned} \|\boldsymbol{\omega}_i\|=1,\boldsymbol{\omega}_i^{T}\boldsymbol{\omega}_j=0,i\neq j \end{aligned}$

が成り立っていることを注意しておく。
　このときもとの変数の線形結合で表される $p$ 個の主成分とその分散は

$\begin{aligned} 第1主成分\ \ y_1&=\boldsymbol{\omega}_1^{T}\boldsymbol{X},&V[Y_1]=\lambda_1,\\ 第2主成分\ \ y_2&=\boldsymbol{\omega}_2^{T}\boldsymbol{X},&V[Y_2]=\lambda_2,\\ &\vdots&\\ 第p主成分\ \ y_p&=\boldsymbol{\omega}_p^{T}\boldsymbol{X},&V[Y_p]=\lambda_p\\ \end{aligned}$

で与えられる。
　主成分分析を適用することで、もとの $p$ 個の変数について観測された $n$ 個の $p$ 次元データ $\{\boldsymbol{X}_i=(X_{i1},\cdots,X_{ip})^{T}; i=1,2,\cdots,n\}$ を $k(\leq n)$ 次元へと縮約できる。高次元データを1次元直線、2次元平面または3次元空間へと射影してデータ構造を視覚的に把握するとともに、元の変数の線形結合として合成された新たな変数のもつ意味を見出すことによって有益な情報抽出が可能になる。
　合成された主成分の持つ意味は、各変数の係数 $\omega_{ij}$ の大きさや政府を通して把握できる。他方で定量的な指標として主成分と各変数の相関を求めておけば、主成分に影響する変数を特定するのに有用である。
　一般に第 $i$ 主成分 $Y_i$ と第 $j$ 番目の変数 $X_j$ との間の相関は

$\begin{aligned} r_{Y_i,X_j}&=\displaystyle{\frac{\mathrm{Cov}[Y_i,X_j]}{\sqrt{V[Y_i]}\sqrt{V[X_j]}}}\\ &=\displaystyle{\frac{\lambda_i\omega_{ij}}{\sqrt{\lambda_i}\sqrt{s_{jj}}}}\\ &=\displaystyle{\frac{\sqrt{\lambda_i}\omega_{ij}}{\sqrt{s_{jj}}}},i,j=1,2,\cdots,p \end{aligned}$

で与えられる。ここで $\lambda_i$ は第 $i$ 主成分の分散、 $\omega_{ij}$ は第 $i$ 主成分を構成する変数 $X_j$ の係数、 $s_{jj}$ は変数 $X_j$ の分散である。

5.3　対称行列の固有値と固有ベクトル

　標本分散共分散行列

は $p\times p$ 次対称行列で、その固有値および固有ベクトルの間には以下が成り立つ：

$\begin{aligned} S\boldsymbol{\omega}_i&=\lambda_i\boldsymbol{\omega}_i,\\ \boldsymbol{\omega}_i^{T}\boldsymbol{\omega}_i&=1,\\ \boldsymbol{\omega}_i^{T}\boldsymbol{\omega}_j&=0,i\neq j,i,j=1,2,\cdots,p \end{aligned}$

　いま $p$ 個の固有ベクトルを列ベクトルとする $p\times p$ 行列を $W$ 、固有値を対角成分に持つ $p\times p$ 対角行列を $\Lambda$ とする。すなわち

$\begin{aligned} W&=(\boldsymbol{\omega}_1,\cdots,\boldsymbol{\omega}_p),\\ \Lambda&=\begin{bmatrix}\lambda_1&0&\cdots&0\\0&\lambda_2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\lambda_p\end{bmatrix} \end{aligned}$

とする。このとき標本分散共分散行列 $S$ の固有値と固有ベクトルの関係は

$\begin{aligned} (1)&\ \ SW=W\Lambda,W^{T}W=I_p,\\ (2)&\ \ W^{T}SW=\Lambda,\\ (3)&\ \ S=W\Lambda W=\displaystyle{\sum_{i=1}^{p}\lambda_i\boldsymbol{\omega}_i\boldsymbol{\omega}_i^{T}},\\ (4)&\ \ \mathrm{tr}S=\mathrm{tr}\left(W\Lambda W^{T}\right)=\mathrm{tr}\Lambda=\displaystyle{\sum_{i=1}^{p}\lambda_i} \end{aligned}$

である。(2)式は対称行列 $S$ は直交行列 $W$ によって対角化可能であることを示しており、(3)式は対称行列 $S$ のスペクトル分解と呼ばれている。また(4)式はもとの変数 $X_1,\cdots,X_p$ の分散の総和 $\mathrm{tr}S=\displaystyle{\sum_{i=1}^{p}s_{ii}}$ が新たに構成した $p$ 個の主成分の分散の総和 $\mathrm{tr}\Lambda=\displaystyle{\sum_{i=1}^{p}\lambda_i}$ に等しいことを表す。

5.4　多次元データの基準化と標本相関係数

　観測された $n$ 個の $p$ 次元データを

$\begin{aligned} \boldsymbol{X}_i=(X_{i1},\cdots,X_{ip})^T,i=1,2,\cdots,n \end{aligned}$

とするとき、 $n$ 個の $p$ 次元データに基づく標本平均ベクトル $\bar{\boldsymbol{X}}=(\bar{X}_1,\cdots,\bar{X}_p)^{T}$ と標本分散共分散行列 $S=(s_{jk})$ を求める。次に上式の第 $i$ 番目の $p$ 次元データを

$\begin{aligned} \boldsymbol{Z}_i=(z_{i1},\cdots,z_{ip})^{T},z_{ij}=\displaystyle{\frac{x_{ij}-\bar{x}_j}{\sqrt{s_{jj}}}},j=1,2,\cdots,p \end{aligned}$

により規格化する。このように規格化された $n$ 個の $p$ 次元データに基づいて標本分散 $(s_{jj})$ と標本共分散 $(s_{jk})$ を計算すると、

$\begin{aligned} s_{jk}^{*}&=\displaystyle{\frac{1}{n}\sum_{i=1}^{n}z_{ij}z_{jk}}\\ &=\displaystyle{\frac{1}{n}\sum_{i=1}^{n}\frac{(x_{ij}-\bar{x}_j)(x_{ik}-\bar{x}_k)}{\sqrt{s_{jj}}\sqrt{s_{kk}}}}\\ &=\displaystyle{\frac{s_{jk}}{\sqrt{s_{jj}}\sqrt{s_{kk}}}}\equiv r_{jk} \end{aligned}$

である。したがって規格化したデータに基づく標本分散共分散行列は、対角成分 $r_{jj}$ がすべて $1$ で、非対角成分 $r_{jk}$ が $j$ 番目と $k$ 番目の変数間の標本相関係数からなる $p$ 次正方行列

$\begin{aligned} R=(r_{jk})=\begin{bmatrix} 1&r_{12}&\cdots&r_{1p}\\ r_{21}&1&\cdots&r_{2p}\\ \vdots&\vdots&\ddots&\vdots\\ r_{p1}&r_{p2}&\cdots&1 \end{bmatrix} \end{aligned}$

に等しく、これを標本相関行列という。
　規格化した多次元データから出発する主成分分析は標本相関行列の固有値問題に帰着され、主成分を導出する過程は標本分散共分散行列から出発する場合と同様である。

5.5　次元圧縮と情報損失

　主成分を用いて高次元空間に散らばるデータの次元を我々の直感で捉えることができる1次元直線、2次元平面または3次元空間へと圧縮することにより、視覚的に高次元データ構造を捉えることができる。ただし高次元データを低次元の空間へと圧縮すると情報の損失が生じることから、次元圧縮による情報損失を定量的に把握しておく必要がある。
　情報損失の例を述べる。2科目の試験において $(60点,80点),(80点,60点)$ というデータを $y=x_1+x_2$ 軸へ射影することで圧縮するとどちらも $140$ となるため、区別が出来なくなる。この損失をできるだけ少なくするために射影したデータが最も散らばる軸を探していると言える。
　主成分分析は情報の量を分散で捉えているため、求めた主成分の分散の相対的な大きさを見れば情報の損失を定量的に把握できる。すでに示したように第 $i$ 主成分の分散 $V[s_{Y_i}^2]=V[Y_i]=\lambda_i$ と対応する固有値で表されたから、もとの $p$ 個の変数 $X_1,\cdots,X_p$ のもつ情報の中で、第 $i$ 主成分 $Y_i$ にはどの程度の情報が含まれている情報の量を測るための基準は、

$\begin{aligned} \displaystyle{\frac{\lambda_i}{\lambda_1+\lambda_2+\cdots+\lambda_p}} \end{aligned}$

で与えられ、寄与率という。また第 $1$ 主成分から第 $k$ 主成分までを用いたときの情報の量は

$\begin{aligned} \displaystyle{\frac{\lambda_1+\cdots+\lambda_k}{\lambda_1+\lambda_2+\cdots+\lambda_p}} \end{aligned}$

で与えられ、累積寄与率という。
　固有ベクトルを列ベクトルとする $W\in\mathbb{R}^{p\times p}$ および固有値を対角成分にもつ $\Lambda\in\mathbb{R}^{p\times p}$ 、すなわち

$\begin{aligned} W&=(\boldsymbol{\omega}_1,\boldsymbol{\omega}_2,\cdots,\boldsymbol{\omega}_p),\\ \Lambda&=\begin{bmatrix} \lambda_1&0&\cdots&0\\ 0&\lambda_2&\cdots&0\\ \vdots&\vdots\ddots&\vdots\\ 0&0&\cdots&\lambda_p \end{bmatrix} \end{aligned}$

に対して

$\begin{aligned} \mathrm{tr}S=\mathrm{tr}\Lambda \end{aligned}$

が得られるから、もとの変数 $X_1,X_2,\cdots,X_p$ のもつ全情報（＝各変数の分散の総和 $\mathrm{tr}S$ ）は $p$ 個の主成分 $Y_1,\cdots,Y_p$ の全情報 $\mathrm{tr}\Lambda$ へと受け継がれるが、次元圧縮により一部の主成分を用いたときには情報の損失が生じる。そのために用いる主成分にどの程度の情報が含まれているかを定量に測るために、全主成分の分散の総和に対する各主成分の分散の相対的な割合を情報損失の基準としていると言える。

5.6　Rによる分析結果

　データとして $\mathrm{iris}$ を用いて主成分分析を行ってみる。

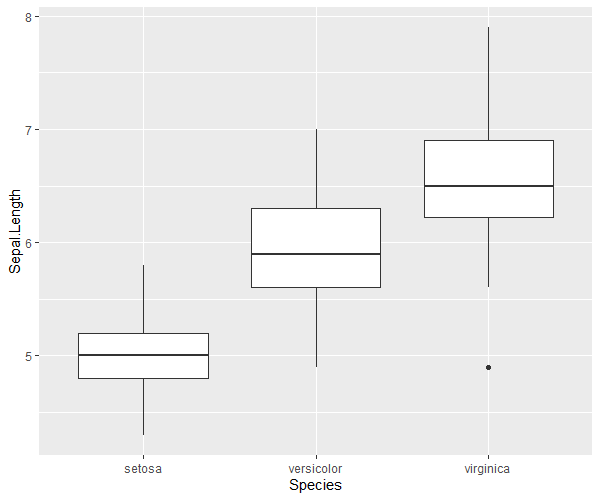
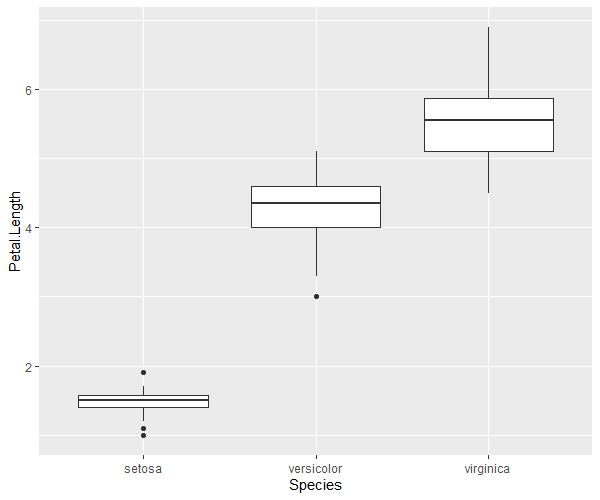
サンプルデータの分布

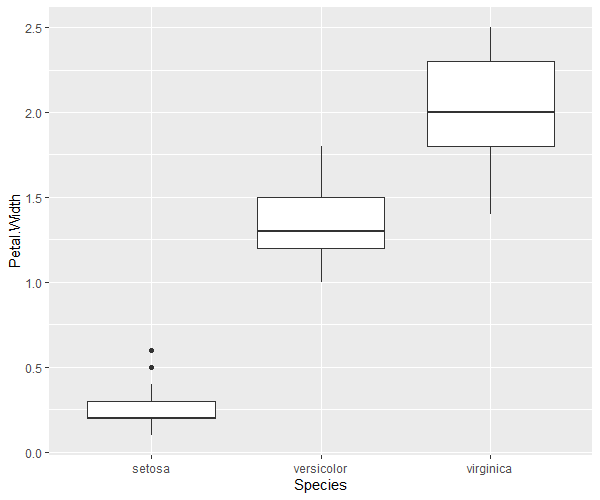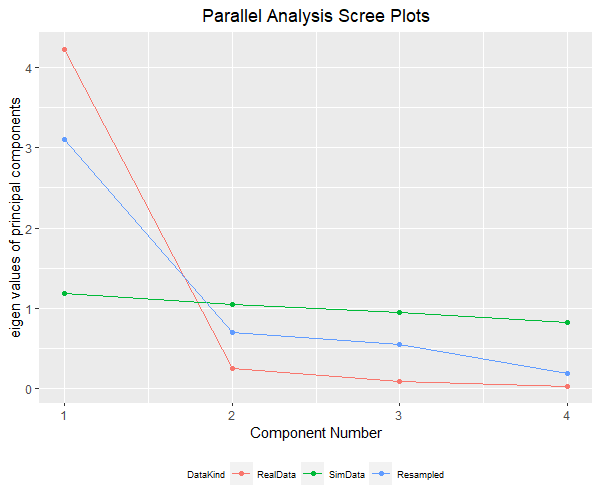
# library(stats) # statsは読込不要

# サンプルデータはiris
data(iris)

# まずはサンプルデータの概形を分析
library(ggplot2)
library(ggrepel)

# Speciesごとに統計量を算出
for(species in unique(iris[,"Species"])){
  print(summary(iris[iris[,"Species"]==species,]))
}

# 列ごとに図示
ggplot(iris,aes(x = Species, y = Sepal.Length)) + geom_boxplot()
ggplot(iris,aes(x = Species, y = Sepal.Width)) + geom_boxplot()
ggplot(iris,aes(x = Species, y = Petal.Length)) + geom_boxplot()
ggplot(iris,aes(x = Species, y = Petal.Width)) + geom_boxplot()

# 主成分分析を実施
ls_comp <- princomp(iris[,-5], cor = F, scores = T)

ls_comp$sdev # 標準偏差
ls_comp$loadings # 固有ベクトル:空欄は近似的に0
ls_comp$center # 平均
ls_comp$scale # 各変数に適用されたスケール
ls_comp$n.obs # 観測値のサイズ
ls_comp$scores # 主成分データの得点
summary(ls_comp) # 寄与率・累積寄与率

# 第1成分だけで9割近くの寄与度があるため、第1・第2成分のみで主成分を表示
summary(ls_comp) # 寄与率・累積寄与率

df_prin_comp <- data.frame(names = row.names(ls_comp$loadings),ls_comp$loadings[,c(1,2)])
row.names(df_prin_comp) <- NULL

g <- ggplot(df_prin_comp,aes(x = Comp.1,y = Comp.2, label = names)) + 
  geom_point()
g <- g  + geom_label_repel()+ theme(plot.title = element_text(hjust = 0.5),legend.position = "bottom",
                                    legend.title=element_text(size = 7),
                                    legend.text=element_text(size = 7))
plot(g)

# 主成分得点
# 情報を縮約した結果であり、元の変数・個体間の相対的関係に過ぎない
df_prin_comp_2 <- data.frame(labels = iris[,5],ls_comp$scores)

g_pcs <- ggplot(data = df_prin_comp_2, aes(x = Comp.1, y = Comp.2, colour = labels)) + 
  geom_point()
g_pcs <- g_pcs + theme(plot.title = element_text(hjust = 0.5),legend.position = "bottom",
                       legend.title=element_text(size = 7),
                       legend.text=element_text(size = 7))
plot(g_pcs)

# 主成分の数を判定する：ここでは平行分析法
library(psych)
lst_pc_num <- fa.parallel(x = iris[,-5], fa = "pc", cor = "cov", n.iter = 1000, error.bars = F)

# 結果を図示
df_parallell_analysis <- data.frame("NumComp" = 1:length(lst_pc_num$pc.values),
                                    "DataKind" = rep("RealData",length(lst_pc_num$pc.values)),
                                    "Data" = lst_pc_num$pc.values)
df_parallell_analysis <- rbind(df_parallell_analysis,
                               data.frame("NumComp" = 1:length(lst_pc_num$pc.sim),
                                          "DataKind" = rep("SimData",length(lst_pc_num$pc.sim)),
                                          "Data" = lst_pc_num$pc.sim))
df_parallell_analysis <- rbind(df_parallell_analysis,
                               data.frame("NumComp" = 1:length(lst_pc_num$pc.simr),
                                          "DataKind" = rep("Resampled",length(lst_pc_num$pc.simr)),
                                          "Data" = lst_pc_num$pc.simr))

g_pa <- ggplot(data = df_parallell_analysis,aes(x = NumComp, y = Data, colour = DataKind)) + geom_line()
g_pa <- g_pa + ggtitle("Parallel Analysis Scree Plots") + xlab("Component Number") + 
  ylab("eigen values of principal components")
g_pa <- g_pa + geom_point() + theme(plot.title = element_text(hjust = 0.5),legend.position = "bottom",
                                    legend.title=element_text(size = 7),
                                    legend.text=element_text(size = 7))
plot(g_pa)

# 予測：全データの一部を学習データ、残りをテストデータとして予測する
# 学習データの行番号
vc_resampling <- sample(x = 1:nrow(iris),size = as.integer(round(0.5 * nrow(iris))),replace = F)
ls_comp <- princomp(iris[vc_resampling,-5], cor = F, scores = T) # 学習データでの主成分分析

# テストデータで予測
pred_comp <- predict(object = ls_comp, data = iris[-vc_resampling,-5])
pred_comp

主成分(第1成分と第2成分)の散布図

主成分得点の散布図(第1成分と第2成分)

平行分析法*3

補足　スペック情報

エディション	Windows 10 Home
バージョン	20H2
プロセッサ	Intel(R) Core(TM) i5-1035G4 CPU @ 1.10GHz 1.50 GHz
実装 RAM	8.00 GB
システムの種類	64 ビットオペレーティングシステム、x64 ベースプロセッサ
R　バージョン	3.6.3 (2020-02-29)
RStudio　バージョン	1.2.5033

次回

power-of-awareness.com

*1:以降、5.1から5.5までは小西貞則(2010)「多変量解析入門　線形から非線形へ」（岩波書店）　PP.225-236参照。

*2: ${}^{T}$ は転置を表す記号とする。

*3:これで見ると、第1成分のみで十分と言える。

前回

5. 主成分分析

5.1 主成分導出の過程

5.2 標本分散共分散行列の固有値問題と主成分

5.3 対称行列の固有値と固有ベクトル

5.4 多次元データの基準化と標本相関係数

5.5 次元圧縮と情報損失

5.6 Rによる分析結果

補足 スペック情報

次回