Pythonで学ぶアルゴリズム（14/18） - 「大人の教養・知識・気付き」を伸ばすブログ

　アルゴリズムを学ぶのにPythonの学習も兼ねて

Ｐｙｔｈｏｎで学ぶアルゴリズムとデータ構造 (データサイエンス入門シリーズ)

作者:辻真吾
講談社

Amazon

を参照していく。

前回

power-of-awareness.com

前回
7.　問題を解くための技術
- 7.2　動的計画法

7.　問題を解くための技術

　ナップサック問題を3通りの方法で解いてみる。

7.2　動的計画法

　ナップサック問題を効率的に解く手段の1つとして動的計画法を用いた方法を紹介する。

7.2.1　ナップサック問題への適用

　グラフの最短距離の場合と同様に、ナップサック問題でも問題の一部分のみを見て最適化することを考える。例として、

品物	重さ	値段
品物0	$1$	$2$
品物1	$1$	$4$
品物2	$2$	$10$

という3つの品物を容量 $3$ のナップサックに詰める問題を検討する。
　そのため以下のように行がどの品物までを考慮したか、列がその時点のナップサック容量を表す表を考える。各セルにはそのときの価値を格納する。

	容量0	容量1	容量2	容量3
空	$0$	$0$	$0$	$0$
品物0
品物1
品物2

　まず品物0について、容量 $0$ 以外は品物0を格納するから、価値が増す。

	容量0	容量1	容量2	容量3
空	$0$	$0$	$0$	$0$
品物0	$0$	$2$	$2$	$2$
品物1
品物2

　次に品物1の行について、該当する列には1行1列分だけ左上のセルの値に品物1の価値を加算した結果を格納する。

	容量0	容量1	容量2	容量3
空	$0$	$0$	$0$	$0$
品物0	$0$	$2$	$2$	$2$
品物1	$0$	$4$	$6$	$6$
品物2

　そして品物2の行について、該当する列には1行2列*1分だけ左上のセルの値に品物2の価値を加算した結果を格納する。

	容量0	容量1	容量2	容量3
空	$0$	$0$	$0$	$0$
品物0	$0$	$2$	$2$	$2$
品物1	$0$	$4$	$6$	$6$
品物2	$0$	$4$	$10$	$14$

　この表では価値の推移しか分からず、どの品物を入れたかは別で勘定する必要があるが、これにより最適な値を得られる。

7.2.2　動的計画法の実装例

########################################
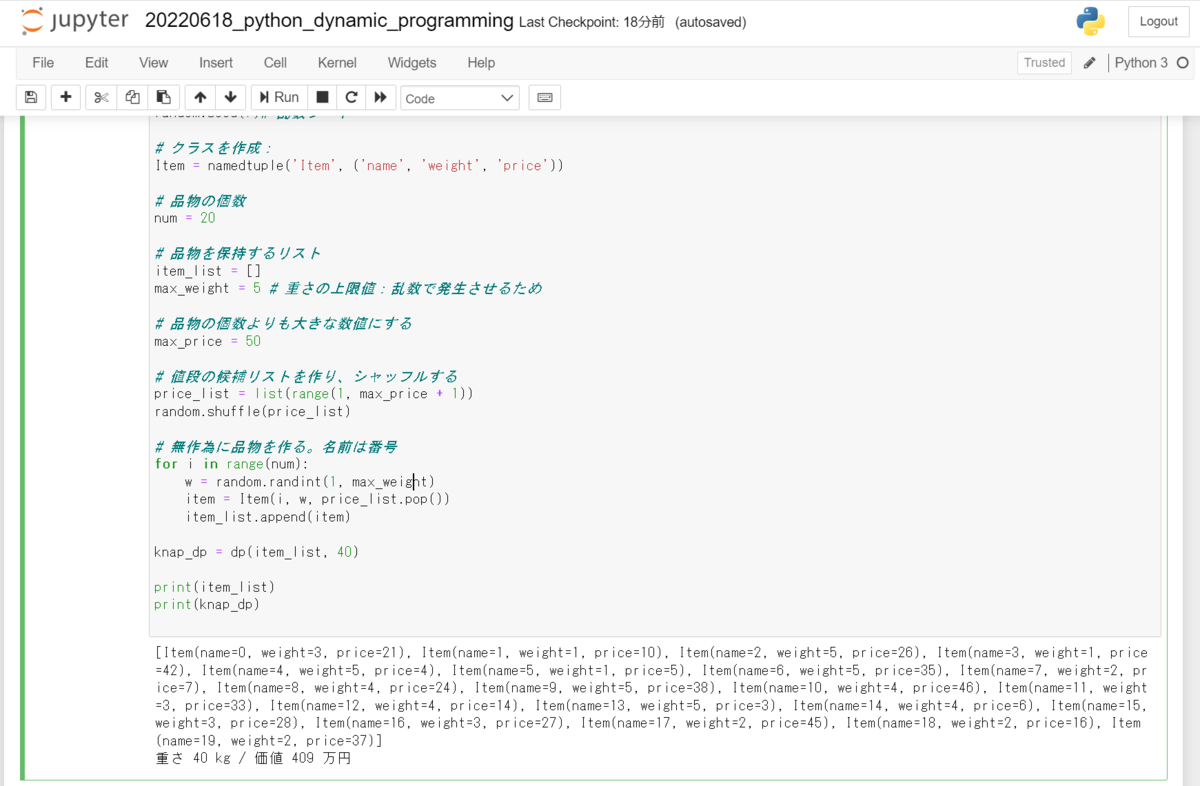
### 動的計画法によるナップサック問題 ###
########################################


### 各種クラスを定義

class Knapsack:
    
    def __init__(self, size):
        # このナップサックが保持できる最大の重さ
        self.size = size
        
        # 現在の重さ
        self.weight = 0
        
        # 入っている品物の価値の総和
        self.value = 0
        
        # 保持するItemの配列
        self.items = []
        
    def append(self, item):
        """ このナップサックにItemを追加する """
        if not self.has_room_for(item):
            raise ValueError('この品物は入れられません。重量オーバーです。')
        self.items.append(item)
        self.weight += item.weight
        self.value += item.price
        
    def has_room_for(self, item):
        """ 引数に取った品物を入れる余裕があるかを真偽値で返す """
        return self.size >= self.weight + item.weight
    
    def __str__(self):
        val = '重さ {} kg / 価値 {} 万円'.format(self.weight, self.value)
        return val

### 動的計画法によるナップサック問題
def dp(items, size_limit):
    n = len(items)
    
    # 価値を記録する表を定義
    table = [[0] * (size_limit + 1) for i in range(n + 1)]
    
    # 価値を更新したかどうかを記録する表
    flg = [[False] * (size_limit + 1) for i in range(n + 1)]
    
    # 表を下に進めていくループ
    for i in range(1, n + 1):
        # 検討中の品物
        target = items[i - 1]
        w = target.weight
        
        # 表を右に進むループ
        for j in range(1, size_limit+1):
            # 1行上の最適解
            yellow = table[i-1][j]
            table[i][j] = yellow
            
            # 現在の許容範囲jを超えるならば次のループへ
            if w > j: continue
            
            # ちょうどtarget分の重さが少ないときの最適解
            pink = table[i-1][j-w]
            
            # この品物を入れた場合の価値
            include_this = target.price + pink
            table[i][j] = max(yellow, include_this)
            flg[i][j] = include_this > yellow
    # 後処理：表を右下から遡って入れた品物を調べる
    i = n
    j = size_limit
    
    my_knapsack = Knapsack(size_limit)
    
    while i > 0 and j > 0:
        if flg[i][j]:
            # この価値更新で追加したのは i-1
            my_knapsack.append(items[i-1])
            
            # 表を左へ戻る
            j -= items[i-1].weight
        i -= 1
    return my_knapsack
    
    
### 品物リストを乱数で作成する

from collections import namedtuple
import random

random.seed(7)# 乱数シード

# クラスを作成：
Item = namedtuple('Item', ('name', 'weight', 'price'))

# 品物の個数
num = 20

# 品物を保持するリスト
item_list = []
max_weight = 5 # 重さの上限値：乱数で発生させるため

# 品物の個数よりも大きな数値にする
max_price = 50

# 値段の候補リストを作り、シャッフルする
price_list = list(range(1, max_price + 1))
random.shuffle(price_list)

# 無作為に品物を作る。名前は番号
for i in range(num):
    w = random.randint(1, max_weight)
    item = Item(i, w, price_list.pop())
    item_list.append(item)

knap_dp = dp(item_list, 40)

print(item_list)
print(knap_dp)