アルゴリズムの学習(004/XXX)

　コンピュータ科学を学ぶべくアルゴリズムを学んでいく。参考として定番書であり古典的名著でもある

［改訂新版］C言語による標準アルゴリズム事典 Software Technology

作者:奥村晴彦
技術評論社

を用いる。実装には勉強もかねてC#を使う。

5.　異性体の数え上げ

　飽和鎖式炭化水素 $C_nH_{2(n+1)}$ の構造異性体の数を数え上げる。水素原子の位置は自然に決まるため、炭素原子のみ考える。
　炭素原子は $1$ 個以上 $4$ 個以下の別の炭素原子と結合できる。ただし結合が環をつくってはならない。

考え方
　結合の手が1本余った基を考える。基はこの余った手で他の炭素原子と結合できる。特殊の場合として炭素原子が $0$ 個の場合も考える。
　空を含む基をちょうど $3$ 個持ってきて、別に用意した $1$ 個の炭素原子の $4$ 本の手のうち $3$ 本と結合させると新しい基ができる。
　空の基を $0$ 番の基とし、空でない基には以下のようにして番号 $1,2,3,\cdots$ を振る。すなわち新しい基はそれを作るのに用いた $3$ 個の基の番号 $(i,j,k)$ を指定することで定まる。ただし曖昧さを無くすべく $i\geq j\geq k$ と仮定する。このような組 $(i,j,k)$ の可能な値を辞書式順序に並び替えてこれらの基にそれぞれ $1,2,\cdots$ と番号を振る。
　 $n$ 個の基の炭素原子の数を $size[n]$ とし、 $n$ 番の基の最も長い鎖の炭素原子数を $length[n]$ とする。 $n$ 番の基が組 $(i,j,k)$ で表されるならば、
$\begin{aligned} size[]&=size[i]+size[j]+size[k]+1,\\ length[n]&=length[i]+1 \end{aligned}$
が成り立つ。基が生成できたところでこれをつなげば求める構造が得られる。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace isomers
{
    class Program
    {
        public const int C = 17;
        public const int L = 2558;

        static void Main(string[] args)
        {
            // メモ：定数の定義：[改訂新版]C#ポケットリファレンス P.54

            var size = new int[L];
            var length = new int[L];
            var count = new int[C + 1];

            int i, j, k, h, len, n, si, sj, sk, sh;

            n = 0;
            size[0] = 0;
            length[0] = 0;

            len = 0; // 46行でエラーを起こし得るため、とりあえず値を追加する

            for (i = 0; i < L; i++)
            {
                len = length[i] + 1; if (len > C / 2) break;
                si = size[i] + 1; if (si + len > C) continue;

                for (j = 0; j <= i; j++)
                {
                    sj = si + size[j]; if (sj + len > C) continue;

                    for (k = 0; k <= j; k++)
                    {
                        sk = sj + size[k]; if (sk + len > C) continue;
                        if (++n >= L) Environment.Exit(1);
                        size[n] = sk;
                        length[n] = len;
                    }
                }
            }

            if (len <= C / 2) Environment.Exit(1);

            for (i = 0; i <= n; i++)
            {
                si = size[i];

                for (j = 0; j <= i; j++)
                {
                    if (length[i] != length[j]) continue;
                    sj = si + size[j]; if (sj > C) continue;
                    count[sj]++;

                    for (k = 0; k <= j; k++)
                    {
                        sk = sj + size[k] + 1; if (sk > C) continue;

                        for (h = 0; h <= k; h++)
                        {
                            sh = sk + size[h];
                            if (sh <= C) count[sh]++;
                        }
                    }

                }
            }

            for(i = 1; i <= C; i++)
            {
                Console.WriteLine("炭素原子が{0}個のものは{1}種類あります。", i, count[i]);
            }
        }
    }
}

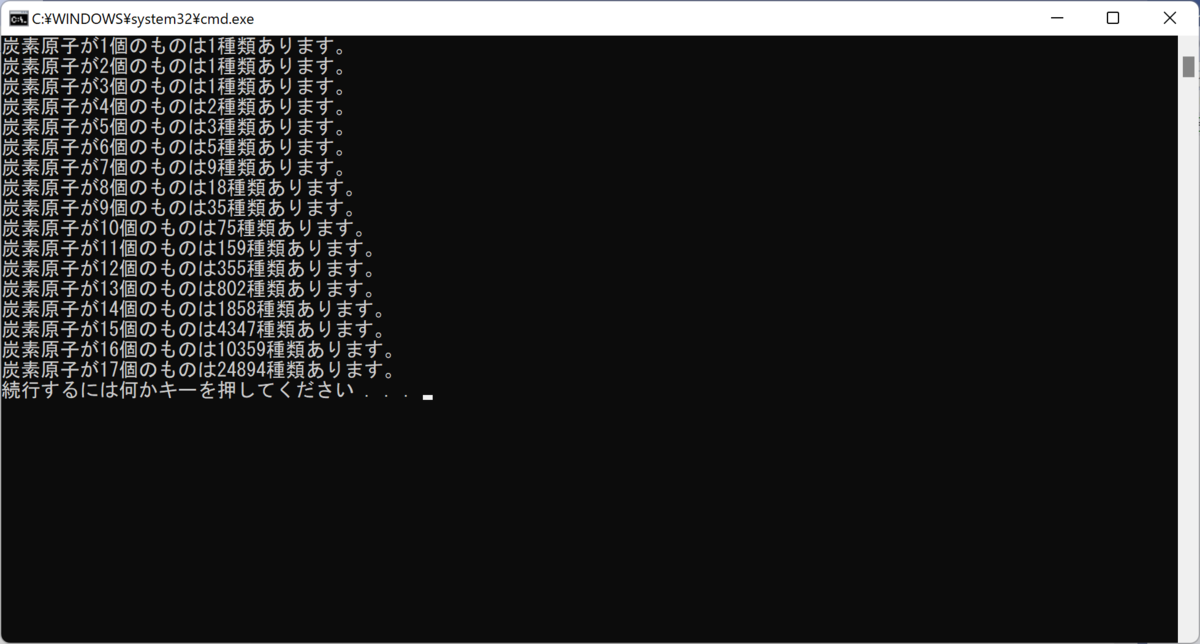
　結果は以下のとおり：

5. 異性体の数え上げ

5.　異性体の数え上げ