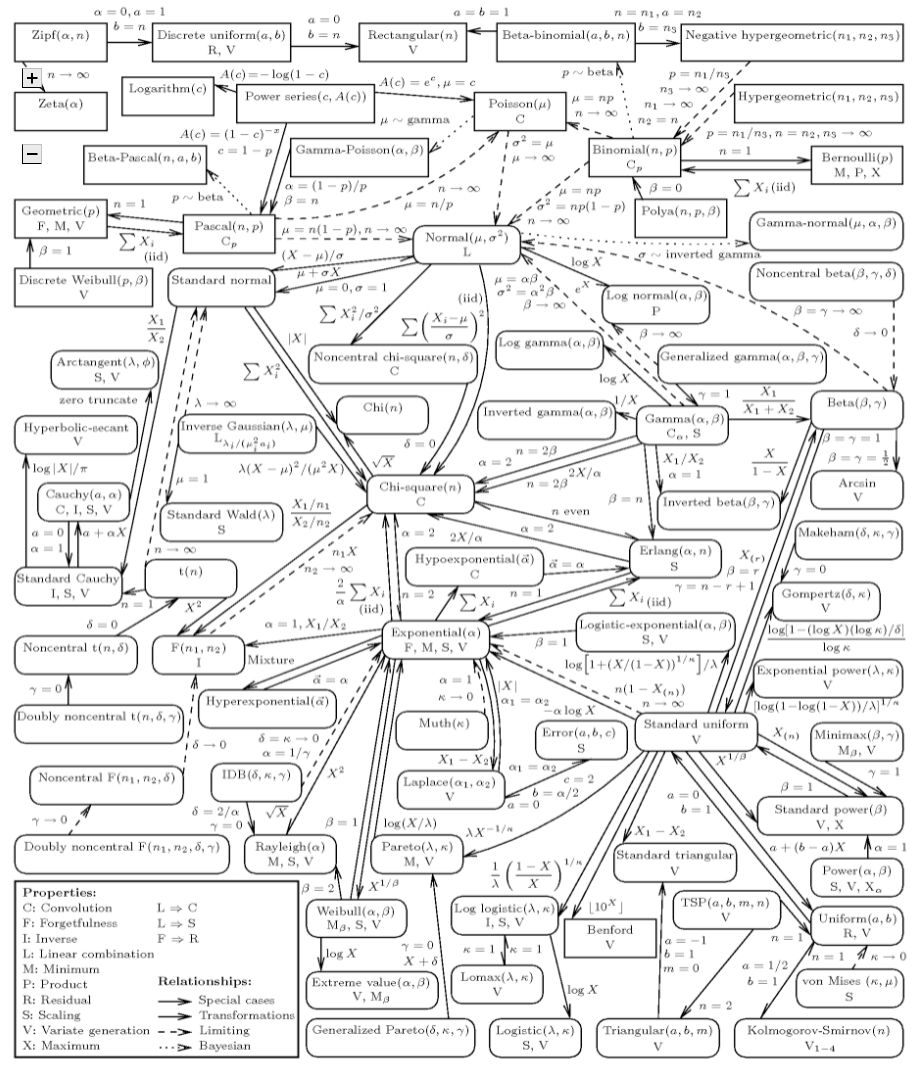
統計学を真剣に学ぶ人のために、個人的にまとめているノートを公開する。
底本として
を用いる。
前回
3. 代表的な一次元確率分布
有名な1次元確率分布を紹介する。代表値の値や特徴的な性質についても同様に述べることとする。
全体に共通して利用できる公式を導出しておく。すなわち
が成り立つ。
( 確率変数
に対して
(離散の場合)
(連続の場合)
3.1 離散型確率分布
まずは離散の場合について述べる。
3.1.1 一様分布
有限個(個)の異なる値
をそれぞれ等確率で取る確率変数
の確率関数が
と書けるとき確率変数は一様分布
に従うという。
- 確率質量関数の確認
- 平均:
- 分散:
3.1.2 二項分布
確率変数の確率質量関数が
と書けるとき確率変数は二項分布
に従うという*2。
のときを特にベルヌーイ分布という。
二項分布はそれぞれが独立で成功確率がであるような試行を
回繰り返すときに成功回数が
回となる確率を表現する分布である。
- 確率質量関数の確認
- 平均:
- 分散:
に注意すれば、
3.1.3 ポアソン分布
確率変数の確率質量関数が
と書けるとき確率変数はポアソン分布
に従うという。
二項分布においてとおき
を一定としつつ
とする(
)と
と導出できる。すなわちポアソン分布は稀にしか起こりえない事象について何回それが生じたのかを観測したときの総生起回数を表す分布であると解釈できる。
- 確率質量関数の確認
- 平均:
- 分散:
より
3.1.4 幾何分布
確率変数の確率質量関数が
と書けるとき確率変数は幾何分布
に従うという。幾何分布は定性的には2つの結果しか生じ得ず毎回の試行が独立であるような事象を行うときに一方の結果が
回目に初めて生じるときの確率である。
- 確率質量関数の確認
- 平均:
ここでとおくと
- 分散:
が成り立つ。ここで
の両辺をで2回微分すると
を得る。両辺にを掛けて
を代入することで
を得る。
3.1.5 超幾何分布
確率変数の確率質量関数が
と書けるとき確率変数は超幾何分布
に従うという。定性的には2つのもの(性質)が合計
個ありそのうち一方が
個あるとする。このとき
個から
個取り出したときにその一方が
個得られる確率を意味する。
- 確率質量関数の確認
ここで二項定理から
である。(*)のの係数と(**)の
の係数とを比較することで
- 平均:
- 分散:
である。右辺第1項は
である。
3.1.6 負の二項分布
確率変数の確率質量関数が
と書けるとき確率変数は負の二項分布
に従うという。定性的にはこれは確率
で成功するような試行が
回成功するまでに
回試行を行うときの確率を意味する。またそれは
回の試行において
回成功したうえで
回目が失敗することを意味するので
とも書ける。
- 確率質量関数の確認
である。これをとおくと
である。また
- 平均:
- 分散:
である。ここで
が成り立つ。以上から
3.1.7 負の超幾何分布
確率変数の確率質量関数が
と書けるとき確率変数は負の超幾何分布
に従うという。
負の超幾何分布は総数個のうち
個が何らかの属性を持つ集団から
個取り出したときに属性を持つ個数が
個含まれ、次に属性を持つ要素が取り出される確率を表す。
3.1.8 対数分布
確率変数の確率質量関数が
と書けるとき確率変数は対数分布
に従うという。
- (1)確率質量関数の確認
である。ここでをMaclaurin展開することで
であるから、
が得られる。
- (2)平均:
- (3)分散:
に対して、
である。とおくと、
であり、したがって
参考文献
- Lehmann, E.L., Casella, George(1998), "Theory of Point Estimation, Second Edition", (Springer)
- Lehmann, E.L., Romano, Joseph P.(2005), "Testing Statistical Hypotheses, Third Edition", (Springer)
- Sturges, Herbert A.,(1926), "The Choice of a Class Interval", (Journal of the American Statistical Association, Vol. 21, No. 153 (Mar., 1926)), pp. 65-66
- 上田拓治(2009)「44の例題で学ぶ統計的検定と推定の解き方」(オーム社)
- 大田春外(2000)「はじめよう位相空間」(日本評論社)
- 小西貞則(2010)「多変量解析入門――線形から非線形へ――」(岩波書店)
- 小西貞則,北川源四郎(2004)「シリーズ予測と発見の科学2 情報量基準」(朝倉書店)
- 小西貞則,越智義道,大森裕浩(2008)「シリーズ予測と発見の科学5 計算統計学の方法」(朝倉書店)
- 佐和隆光(1979)「統計ライブラリー 回帰分析」(朝倉書店)
- 清水泰隆(2019)「統計学への確率論,その先へ ―ゼロからの速度論的理解と漸近理論への架け橋」(内田老鶴圃)
- 鈴木 武, 山田 作太郎(1996)「数理統計学 基礎から学ぶデータ解析」(内田老鶴圃)
- 竹内啓・編代表(1989)「統計学辞典」(東洋経済新報社)
- 竹村彰通(1991)「現代数理統計学」(創文社)
- 竹村彰通(2020)「新装改訂版 現代数理統計学」(学術図書出版社)
- 東京大学教養学部統計学教室編(1991)「基礎統計学Ⅰ 基礎統計学」(東京大学出版会)
- 東京大学教養学部統計学教室編(1994)「基礎統計学Ⅱ 人文・社会科学の統計学」(東京大学出版会)
- 東京大学教養学部統計学教室編(1992)「基礎統計学Ⅲ 自然科学の統計学」(東京大学出版会)
- 豊田秀樹(2020)「瀕死の統計学を救え! ―有意性検定から「仮説が正しい確率」へ―」(朝倉書店)
- 永田靖(2003)「サンプルサイズの決め方」(朝倉書店)
- 柳川堯(2018)「P値 その正しい理解と適用」(近代科学社)
*1:Univariate Distribution Relationship Chart参照。
*2:と書くこともある。