を使うのに、今一度
で使い方を整理する。
前回
注意
参照文献はかなり古い(2019年)ため、現在のバージョンでは動作しない関数などが多いとの評判がある。そこでそういった齟齬があった場合は随時コメントする。なお筆者の環境は、
| アプリケーション | バージョン |
|---|---|
である。
0. まえがき
1. データ構造とアルゴリズム
に組み込まれた機能を利用しつつ実用的なカスタムアルゴリズムを実装する方法を紹介する。
1.1 配列中の最小要素のインデックスを取得する
組み込み関数のはコレクションの中の最小よそのインデックスを取得する。しかし最小要素が複数ある場合、最初の要素しか返さない。
#################################### ### 最小要素のインデックスを返す ### #################################### test = [1, 2, 3, 1, 2, 3] # 組み込み関数:最小要素が複数ある場合には最初のインデックスを返す # argmin println(argmin(test)) # 自作関数:最小要素が複数ある場合にすべてのインデックスを返す # allargmin function allargmin(a) m = minimum(a) filter(i -> a[i] == m, eachindex(a)) end println(allargmin(test)) # 自作関数:最小要素が複数ある場合にすべてのインデックスを返す # randargmin1 function randargmin1(a) rand(allargmin(a)) end println(randargmin1(test)) # 自作関数:最小要素が複数ある場合にすべてのインデックスを返す # randargmin2 function randargmin2(a) indices = eachindex(a) y = iterate(indices) y === nothing && throw(ArgumentError("Collection must be non-empty")) (idx, state) = y minval = a[idx] bestidx = idx bestcount = 1 y = iterate(indices, state) while y !== nothing (idx, state) = y curval = a[idx] if isless(curval, minval) minval = curval bestidx = idx bestcount = 1 elseif isequal(curval, minval) bestcount += 1 rand() * bestcount < 1 && (bestidx = idx) end y = iterate(indices, state) end bestidx end println(randargmin2(test))
1.1.1 iterate
関数は、イテラブルをこの関数に渡すと、以下の2つを格納したタプルを返す。
- イテラブルの最初の要素
- 以降の呼び出しで使うための状態変数
を返す。2つ目の返り値は、ループをしているときに、関数の第2引数として渡してやることでループを進めることができるものである。
######################### ### iterate関数の挙動 ### ######################### x = [6,2,7,1,2,3,1,2] #動作検証 itarateにiteratorとindexを与える: iterate(iterator, index) xi = iterate(x) x1 = iterate(x,1) x2 = iterate(x,2) x3 = iterate(x,3) x4 = iterate(x,4) x5 = iterate(x,5) x6 = iterate(x,6) x7 = iterate(x,7) x8 = iterate(x,8) x9 = iterate(x,9) #表示 @show(xi) @show(x1) @show(x2) @show(x3) @show(x4) @show(x5) @show(x6) @show(x7) @show(x8) @show(x9) @show(iterate(x,iterate(x)[2]))
1.1.2 islessやisequalを用いる訳
でも、
や
のように
や
などを用いることができる。しかし
が渡されたときに
を返すという難点がある。その点、
や
を用いれば、
を渡しても
型が返ってくることが保障される。
1.2 行列乗算を高速に行う
行列を
行列に掛けて
行列を得る場合、この操作の計算複雑性は
である。したがって複数の行列を連続して掛ける場合、その計算量は乗算を行なう順番によって変わる。
たとえば
:
:
:
に対して積を計算したいとする。このとき
という順番で計算することも、
と計算することもできる。しかし前者では
に比例する一方で後者は
に比例し、計算の順序で計算コストが大いに変わり得る。
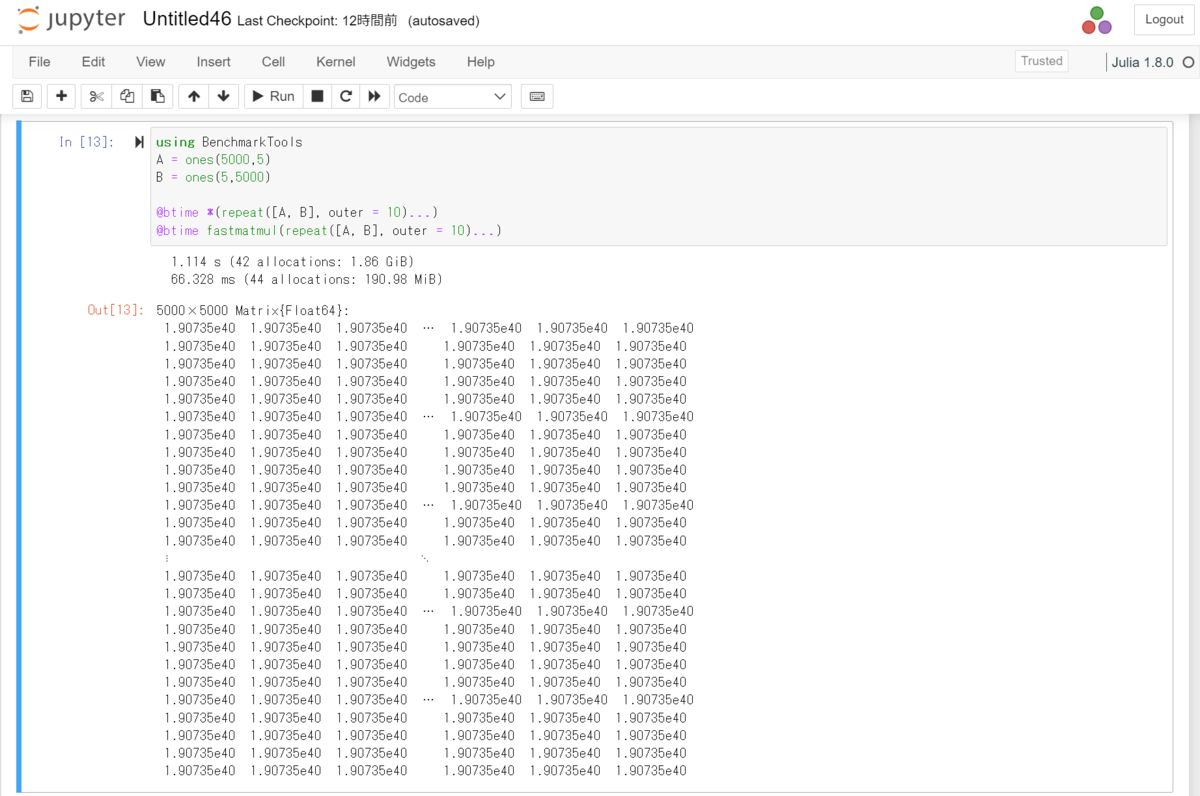
########################################## ### 高速な行列乗算機能を持つ関数を定義 ### ########################################## function fastmatmul(args::AbstractMatrix...) """ 最も計算効率の良い順序で行列積を計算する """ length(args) ≤ 1 && return *(args...) sizes = size.(args) if !all(sizes[i][2] == sizes[i+1][1] for i in 1:length(sizes) -1) throw(ArgumentError("matrix dimensions mismatch")) end partcost = Dict{Tuple{Int,Int}, Tuple{Int,Int}}() from, to = 1, length(sizes) solvemul(sizes, partcost, from, to) domul(args, partcost, from, to) end function solvemul(sizes, partcost, from, to) """ 最適な乗算順序を見つける """ if from == to partcost[(from, to)] = (0, from) return end mincost = typemax(Int) minj = -1 for j in from:to-1 haskey(partcost, (from, j)) || solvemul(sizes, partcost, from, j) haskey(partcost, (j+1, to)) || solvemul(sizes, partcost, j+1, to) curcost = sizes[from][1] * sizes[j][2] * sizes[to][2] + partcost[(from, j)][1] + partcost[(j+1, to)][1] if curcost < mincost minj = j mincost = curcost end end partcost[(from, to)] = (mincost, minj) end function domul(args, partcost, from, to) """ 予め計算した最適な順番で乗算を行なう """ from == to && return args[from] from + 1 == to && return args[from] * args[to] j = partcost[(from, to)][2] domul(args, partcost, from, j) * domul(args, partcost, j+1, to) end ##### # 参考文献のままA = ones(5,5000),B = ones(5000,5)としたらパフォーマンスに相違が無かったので変更 using BenchmarkTools A = ones(5000,5) B = ones(5,5000) @btime *(repeat([A, B], outer = 10)...) @btime fastmatmul(repeat([A, B], outer = 10)...)