をプログラムとして見たときに注意・検討すべきところを学んでおきたい、ということで
を読んでいく。
前回
3. 行列と配列
行列は行数と列数の2つの属性を付与したベクトルである。行列はより一般的なオブジェクトである配列の特殊な例でもある。
3.1 行列の作成
行列は内部的に列優先順で格納する。行優先にするには、そのための引数に値を与える。
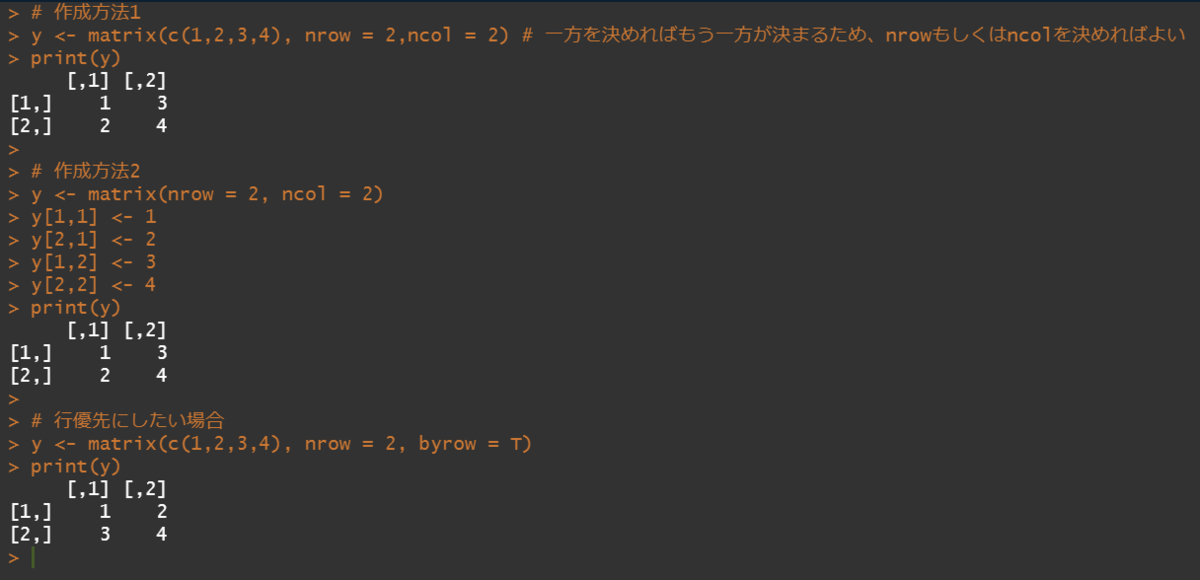
# 作成方法1 y <- matrix(c(1,2,3,4), nrow = 2,ncol = 2) # 一方を決めればもう一方が決まるため、nrowもしくはncolを決めればよい print(y) # 作成方法2 y <- matrix(nrow = 2, ncol = 2) y[1,1] <- 1 y[2,1] <- 2 y[1,2] <- 3 y[2,2] <- 4 print(y) # 行優先にしたい場合 y <- matrix(c(1,2,3,4), nrow = 2, byrow = T) print(y)
 |
3.2 一般的な行列操作
行列で実行できる一般的な操作を紹介する。
3.2.1 線形代数的な演算処理
行列に対しては、行列の乗算、スカラ倍および加算などの線形代数演算を行うことができる。
################## ### 行列の演算 ### ################## # 行列の乗算 y %*% y # スカラ倍 10 * y # 行列の加算 y + y
3.2.2 行列のインデックス付け
ベクトルの操作と同じ操作を行列にも適用できる。
############################## ### 行列のインデックス付け ### ############################## z <- matrix(c(1,2,3,4,1,1,0,0,1,0,1,0),nrow = 4) z[,2:3] # 2列目と3列目のブロック行列を抽出 z[2:3,2] # 2行目と3行目の各2番目の成分 # 部分行列への値の割り当て y <- matrix(1:6,nrow = 3) y y[c(1,3),] <- matrix(c(1,1,8,2),nrow = 2) y # 負の添字は行列でも可能 y[-1,]
3.2.3 行列のフィルタリング
行列でもフィルタリングを行なうことができる。
### x <- matrix(c(1,2,3,2,3,4),nrow = 3) x[x[,2]>=3,] # 2列目が3以上の行を返す (x[,2]>=3)
パフォーマンスを考える上では、行のインデックスを得るブール値ベクトルが完全にベクトル化された演算であることに注目すべきである。
- オブジェクト
はベクトルである。
- 演算子
は2つのベクトルを比較する。
- 数値
は成分として
を持つベクトルにリサイクルされている。
ここまでは行抽出を述べたが、列抽出も同様に利用できる。
上記のフィルタリング*1ではベクトルが得られ、データ型の面では部分行列が得られるわけではない。そのため別の行列関数に渡す場合などには問題が起こり得るため、引数(別章にて記述)を用いる。
3.3 行列の行と列への関数適用
3.3.1 apply()関数の使用
行列に対するの一般的な形式は以下のとおりである。
apply(m, dimcode,f,fargs)
| 行列 | ||
| 次元。関数を行に適用するには |
||
| 適用する関数 | ||
z <- matrix(1:6,nrow = 3) apply(z,1,mean)
関数がスカラを返す場合、最終結果はベクトルになる。
3.4 行列の行と列の追加と削除
行列は長さと次元が固定であるため、行れや列の追加および削除は出来ない。しかし行列は再割り当てにより、直接追加や削除を行う場合と同じ効果を得られる。
ベクトルと同様に、再割り当てによりサイズを変更できる。たとえばを用いると行列に行や列を追加できる。
one <- rep(1,4) z <- matrix(c(1,2,3,4,1,1,0,0,1,0,1,0),nrow = 4) cbind(z,one) # リサイクルも活用できる cbind(1,z)
注意すべきなのは、以下のコードではは新しい行列を作成するのに等しい。これは
に新しい行列を再割り当てしている。そのためループ内でこの処理を繰り返すと、累積して大きなロスになる。
z <- cbind(one,z)
3.5 ベクトルと行列の相違
行列は、行数と列数の属性を付加した単なるベクトルである。ここでは行列が持つベクトルの性質を取り上げる。
まずベクトルであるため、で長さを取得できる。他方で
クラスに所属するため、
関数でも取得できる。
z <- matrix(1:8,nrow=4) length(z) # ベクトルであるから長さが取得できる class(z) attributes(z)
また行数と列数は、
で取得できる。
z <- matrix(1:8,nrow=4) nrow(z) ncol(z)
3.6 予期しない次元削減の回避
統計分析では一般に次元削減は歓迎できる。しかし目的によっては次元削減をしたくない場合もある。
たとえば4行の行列から行を抽出したいとする。これはの行列ではなく、長さ
のベクトルであることである。この意味で次元削減が生じてしまう。
z <- matrix(1:8,nrow=4) r <- z[2,] r # このrはベクトル # attributes(z) str(z) str(r)
ベクトルになったために、後段の処理に問題が生じる場合がある*2。
もし行列のままで処理したい場合、引数を用いる。
z <- matrix(1:8,nrow=4) r <- z[2,, drop = F]
3.7 行列の行・列への名前付け
行列の行・列にはそれぞれ()関数および
()関数で名前を付けることができる。
z <- matrix(c(1:6),nrow = 3) rownames(z) <- c("A","B","C") colnames(z) <- c("X","Y")
3.8 高次元配列
行列は2次元データ構造である。とはいえデータによっては3次元データもあり得、このようなデータセットを配列という。
3次元データは()関数を用いて定義する。
################## ### 高次元配列 ### ################## first <- matrix(c(46,30,21,25,50,48), nrow = 3) second <- matrix(c(46,43,41,35,50,50), nrow = 3) ar_tests <- array(data = c(first, second), dim = c(3,2,2)) attributes(ar_tests) ar_tests[3,2,1] #3行2列の1番目(first)の値
